Encontrar la ecuación de una línea recta: Uso de los dos puntos dados

Forma punto-pendiente de una líneaUso del ángulo formado por la línea con los ejes
Ejercicio 1

Halle la ecuación de la recta que pasa por los dos puntos \( (5,0),(\frac{1}{2},4\frac{1}{2}) \)

Ejercicio 2

Halle la ecuación de la recta que pasa por los dos puntos \( (-2,-6),(4,12) \)

Ejercicio 3

Halle la ecuación de la recta que pasa por los dos puntos \( (\frac{1}{3},1),(-\frac{1}{3},2) \)

Ejercicio 4

Halle la ecuación de la recta que pasa por los dos puntos \( (9,10),(99,100) \)

Ejercicio 5

Halle la ecuación de la recta que pasa por los dos puntos \( (2,8),(6,1) \)

ejemplos con soluciones para Encontrar la ecuación de una línea recta: Uso de los dos puntos dados

Ejercicio #1

Halle la ecuación de la recta que pasa por los dos puntos (5,0),(12,412) (5,0),(\frac{1}{2},4\frac{1}{2})

Solución en video

Solución Paso a Paso

Primero, usaremos la fórmula para encontrar la pendiente de la línea recta:

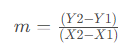
Reemplazamos los datos y resolvemos:

(0−4.5)(5−0.5)=−4.54.5=−1 \frac{(0-4.5)}{(5-0.5)}=\frac{-4.5}{4.5}=-1

Ahora, sabemos que la pendiente es −1 -1

 

Reemplazamos uno de los puntos en la fórmula de la ecuación de la recta:

y=mx+b y=mx+b

(5,0) (5,0)

0=−1×5+b 0=-1\times5+b

 0=−5+b 0=-5+b

b=5 b=5

Ahora tenemos los datos para completar la ecuación:

y=−1×x+5 y=-1\times x+5

y=−x+5 y=-x+5

Respuesta

y+x=5 y+x=5

Ejercicio #2

Halle la ecuación de la recta que pasa por los dos puntos (−2,−6),(4,12) (-2,-6),(4,12)

Solución en video

Respuesta

y=3x y=3x

Ejercicio #3

Halle la ecuación de la recta que pasa por los dos puntos (13,1),(−13,2) (\frac{1}{3},1),(-\frac{1}{3},2)

Solución en video

Respuesta

y=−32x+112 y=-\frac{3}{2}x+1\frac{1}{2}

Ejercicio #4

Halle la ecuación de la recta que pasa por los dos puntos (9,10),(99,100) (9,10),(99,100)

Solución en video

Respuesta

y=x+1 y=x+1

Ejercicio #5

Halle la ecuación de la recta que pasa por los dos puntos (2,8),(6,1) (2,8),(6,1)

Solución en video

Respuesta

y=−134x+1112 y=-1\frac{3}{4}x+11\frac{1}{2}

Ejercicio 1

Halle la ecuación de la recta que pasa por los dos puntos \( (12,40),(2,10) \)

Ejercicio 2

Halle la ecuación de la recta que pasa por los dos puntos \( (15,36),(5,16) \)

Ejercicio 3

Halle la ecuación de la recta que pasa por los dos puntos \( (5,-11),(1,9) \)

Ejercicio #6

Halle la ecuación de la recta que pasa por los dos puntos (12,40),(2,10) (12,40),(2,10)

Solución en video

Respuesta

y−4=3x y-4=3x

Ejercicio #7

Halle la ecuación de la recta que pasa por los dos puntos (15,36),(5,16) (15,36),(5,16)

Solución en video

Respuesta

y=2x+6 y=2x+6

Ejercicio #8

Halle la ecuación de la recta que pasa por los dos puntos (5,−11),(1,9) (5,-11),(1,9)

Solución en video

Respuesta

y+5x=14 y+5x=14