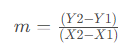Encontrar la ecuación de una línea recta - Ejemplos, Ejercicios y Soluciones

Hallar una ecuación lineal es en realidad graficar la función lineal usando $y=mx+b$ o $y=mx$ .

Podemos hallar la ecuación lineal de $5$ maneras:

Utilizando un punto en la recta y la pendiente de la recta.
Utilizando dos puntos que se encuentran en la recta.
Utilizando la gráfica de la propia función.
Utilizando rectas paralelas, es decir, si la recta solicitada es paralela a otra recta y conocemos la pendiente de la otra recta.
Utilizando rectas perpendiculares, es decir, si la recta solicitada es perpendicular a otra recta y conocemos la pendiente de la otra recta.

Las tres primeras secciones se basan de una forma u otra en la fórmula general para hallar la ecuación lineal:

$y-y1=m\times\left(x-x1\right)$

Las dos últimas secciones también utilizan esta fórmula, pero además tienen en cuenta dos reglas adicionales:

Para las rectas paralelas, las pendientes son iguales, es decir $m1=m2$
Para rectas perpendiculares, para las pendientes existe $m1\times m2=-1$

Explicación completa

Temas sugeridos para practicar con anticipación

Practicar Encontrar la ecuación de una línea recta

Ejercicio 1

Halle la ecuación de la recta que pasa por los dos puntos $(5,0),(\frac{1}{2},4\frac{1}{2})$

Ejercicio 2

Halle la ecuación de la recta que pasa por los dos puntos $$ (-2,-6),(4,12) $$

Ejercicio 3

Halle la ecuación de la recta que pasa por los dos puntos $(\frac{1}{3},1),(-\frac{1}{3},2)$

Ejercicio 4

Halle la ecuación de la recta que pasa por los dos puntos $$ (9,10),(99,100) $$

Ejercicio 5

Halle la ecuación de la recta que pasa por los dos puntos $$ (2,8),(6,1) $$

ejemplos con soluciones para encontrar la ecuación de una línea recta

Ejercicio #1

Halle la ecuación de la recta que pasa por los dos puntos $(5,0),(\frac{1}{2},4\frac{1}{2})$

Solución en video

Solución Paso a Paso

Primero, usaremos la fórmula para encontrar la pendiente de la línea recta:

Reemplazamos los datos y resolvemos:

$\frac{(0-4.5)}{(5-0.5)}=\frac{-4.5}{4.5}=-1$

Ahora, sabemos que la pendiente es $-1$

Reemplazamos uno de los puntos en la fórmula de la ecuación de la recta:

$y=mx+b$

$(5,0)$

$0=-1\times5+b$

$0=-5+b$

$b=5$

Ahora tenemos los datos para completar la ecuación:

$y=-1\times x+5$

Respuesta

$y=-1\frac{3}{4}x+11\frac{1}{2}$

Ejercicio 1

Halle la ecuación de la recta que pasa por los dos puntos $$ (12,40),(2,10) $$

Ejercicio 2

Halle la ecuación de la recta que pasa por los dos puntos $$ (15,36),(5,16) $$

Ejercicio 3

Halle la ecuación de la recta que pasa por los dos puntos $$ (5,-11),(1,9) $$

Ejercicio 4

Recta pasa por el punto $$ (6,14) $$ y paralela a la recta $$ x+3y=4x+9 $$

Ejercicio 5

Recta pasa por el punto $$ (-2,-13) $$ y paralela a la recta $$ -4+y=5x-6 $$

ejemplos con soluciones para encontrar la ecuación de una línea recta

Ejercicio 1

Recta pasa por el punto $$ (-5,12) $$ y paralela a la recta $$ 5y-5x=15 $$

Ejercicio 2

Recta pasa por el punto $$ (0,1) $$ y paralela a la recta $$ 2(y+1)=16x $$

Ejercicio 3

Dadas dos rectas cuya pendiente -3, -6.

¿Cuál de las rectas tiene un ángulo mayor con el eje x?

Ejercicio 4

Dadas dos rectas que tienen su pendiente $2,\frac{1}{2}$ .

¿Cuál de las rectas tiene un ángulo mayor con el eje x?

Ejercicio 5

Dadas dos rectas que tienen su pendiente $-6,\frac{1}{2}$ .

¿Cuál de las rectas tiene un ángulo menor con el eje x?