La suma y la resta de números reales se basan en ciertos principios clave. Se explicarán todos los principios con dos números reales, pero, ciertamente, los números en el ejercicio no influyen al modo de resolución, por lo tanto, se pueden aplicar estos principios a cualquier número del ejercicio.
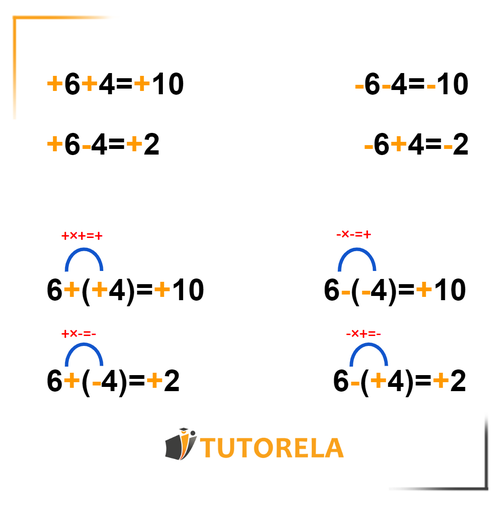
Cuando tenemos dos números reales con el mismo signo (más o menos), este signo permanecerá en el resultado, que será, de hecho, el resultado de la suma. Es decir, si los dos números llevan el signo más el resultado de la adición (suma) también será positivo. Si los dos números llevan el signo menos el resultado de la sustracción (resta) también será negativo.
- Cuando tenemos dos números que llevan signos diferentes es primordial determinar cuál de los dos tiene el mayor valor absoluto (absoluto: la distancia del cero). El número más grande determinará el signo que llevará el resultado y, de hecho, haremos una operación de sustracción.
- Cuando tengamos un ejercicio con una secuencia de dos signos (separados generalmente por paréntesis) diferenciaremos entre varios casos:
- Cuando la secuencia es de dos signos de sumar el resultado también será positivo
- Cuando la secuencia es de dos signos de restar el resultado también será positivo
- Cuando la secuencia es de menos y más o de más y menos el resultado será negativo.