Suma y resta de números reales

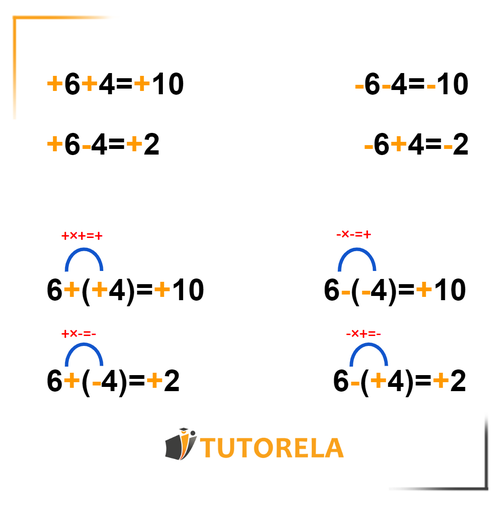
Luego de haber estudiado los números reales ha llegado la hora de aprender cómo utilizarlos en una ecuación. En principio, nuestro objetivo en las ecuaciones es simplificarlas para que nos sea más cómodo resolver los ejercicios, esto lo hacemos agrupando operaciones y sumando y restando números reales. Sólo debemos recordar dos reglas:

• Cuando la operación matemática y el signo del número real siguiente sean del mismo tipo, los agruparemos en una suma.
• Por ejemplo: $5+(+5)$ y $5-(-5)$
  $5+5$ pasarán a ser
   
• Cuando la operación matemática y el signo del número real siguiente sean de diferente tipo, los agruparemos en una operación que dará la diferencia entre ellos. Por ejemplo: $5+(-5)$ y $5-(+5)$
  $5-5$ pasarán a ser 

Por ejemplo:

$10+(+5)-(+3)-(-6)+(-8)=$
$10+5-3+6-8=10$

Hay una táctica muy conocida que ayuda a entender el tema de los números reales de la mejor manera, se llama el método del ascensor y sirve para esclarecer la suma y la resta de números reales. Con este método nos imaginamos que el ejercicio es como un recorrido en elevador que va pasando por los pisos. Observa el siguiente ejercicio:

$-5-(+1)-(-8)+(-3)=$

Antes de utilizar el método del ascensor tenemos que agrupar los signos para simplificar el ejercicio

$-5-1+8-3=$

Ahora mira el primer número. De hecho, comienzas el ejercicio en el piso $-5$ y ahora se te pide bajar un piso. De este modo llegas al piso $-6$.
Ahora te piden que subas $8$ pisos. Entonces, si estábamos en el piso $-6$ llegaremos al piso $2$. Por último, te piden que bajes $3$ pisos, por lo tanto, terminas en el piso $-1$, siendo éste el resultado del ejercicio

$-5-1+8-3=-1$

Daremos consistencia a los principios expuestos a través de los siguientes ejemplos:

$(+3) + (+4) + (+5) = 3+4+5= +12$

$(-3) + (-4) + (-5) = -3-4-5= -12$

$-10+2= -8$

$6-20= -14$

$(-10)-(-100)= -10+100= 90$

$8+(-4)= 8-4= 4$

Si te interesa este artículo también te pueden interesar los siguientes artículos:

Números positivos, negativos y el cero

Inverso multiplicativo

La recta real

Números opuestos

Valor absoluto

Eliminación de paréntesis en números reales

Multiplicación y división de números reales

En la página web de Tutorela encontrarás una variedad de artículos sobre matemáticas.

Consigna

$-27-\left(-7\right)+\left(-6\right)+2-11=$

Solución

Primero resolvemos los puntos de multiplicación, es decir, los puntos que tienen un signo más o menos antes de otro signo.

$-27+7-6+2-11=$

Ahora resolvemos como un ejercicio común:

$-27+7-6+2-11=-35$

Respuesta

$-35$

Consigna

$\text{?}-(-12)=-40$

Solución

Primero prestemos atención que los dos menos se convierten en más.

$\text{?+}12=-40$

Pasaremos al $12$ al lado derecho

$\text{?}=-40-12$

Por último resolvemos

$\text{?}=-52$

Respuesta:

$-52$

Consigna

$-36+6=$

Solución

Usamos las leyes de la suma y resta para resolver en consecuencia.

$-36+6=-30$

Respuesta:

$-30$

$12-\left(-2\right)=$

Solución

Prestar atención a que los signos menos y menos se convierten en más, y resolvemos el ejercicio en consecuencia.

$12+2=14$

Respuesta

$14$

Consigna

Dado que:

$a$ Número negativo

$b$ Número negativo

¿Cuál es la suma de $a+b$?

Solución

Cuando sumamos dos números negativos, el resultado que obtendremos será un número negativo.

Respuesta

Negativo

¿Cómo se suman y se restan los números reales?

Para poder sumar y restar números reales debemos de tener en cuenta algunas reglas para poder realizar las operaciones aritméticas, ya que en este caso nos encontraremos con números negativos y positivos y eso hace un poco diferente el procedimiento que como lo hacíamos con los números naturales.

Cabe mencionar que cuando sumamos y restamos números reales en ocasiones debemos de conocer las leyes de los signos, y esto es importante diferenciarlo a la regla de suma y resta. Nos podemos encontrar con dos casos, el primero es que debemos de sumar o restar números con mismo signo y el segundo con diferente signo.

¿Cómo se suman y restan números con signos iguales?

Cuando tenemos la suma y resta de signos iguales debemos de hacer la operación básica con números reales y conservar el signo que tenemos, es decir, si sumamos dos números positivos se suman normal y el resultado será negativo; si sumamos o restamos dos números negativos, se suman sus valores absolutos y se conserva el signo negativo, el resultado será negativo, veamos algunos ejemplos.

$5+9=14$

$14+26=40$

En este caso los dos números son positivos, sumamos normal y el resultado es positivo.

$-6-8=-14$

$-28-13=-41$

Ahora observamos que los números son negativos, sumamos sus valores absolutos y como son negativos, el resultado es negativo.

¿Cómo se suman y restan números con signos diferentes?

En este caso la regla para poder sumar números con diferente signo es realizar una resta entre ellos y conservar el signo que tiene el mayor valor absoluto, veamos algunos ejemplos:

$16-9=7$

En este ejemplo vemos que el $16$ es positivo y el $9$ negativo (diferentes signos), entonces vamos a restarlos normal, pero podemos observar que el $16$ tiene mayor valor absoluto por lo cual el resultado bebe ser positivo.

$-25+8=-17$

Aquí nuevamente vemos que tienen diferente signo, por lo cual procedemos a restar, al numero más grande le restamos el menor y vemos que el que tiene mayor valor absoluto es el $25$ y como es negativo, entonces el resultado será negativo.

Veamos más ejemplos:

$33-56=-23$

$25-38=-13$

$-14+29=15$

¿Qué es la regla de suma y resta?

Son herramientas que nos ayudan a realizar sumas y restas con números reales, es decir, con números positivos y negativos y nos sean más fácil resolver las operaciones aritméticas. Y las hemos mencionado y aplicado en las preguntas anteriores.