La resolución de una ecuación utilizando la propiedad distributiva está relacionada con la necesidad de abrir los paréntesis como primer paso para después poder simplificar los miembros similares. Cuando una ecuación contiene uno o más pares de paréntesis, debemos comenzar por abrirlos todos y después proseguir con la siguiente fase.
Solución de una ecuación usando la propiedad distributiva - Ejemplos, Ejercicios y Soluciones
A continuación, te dejamos algunos ejemplos donde se aplica este método
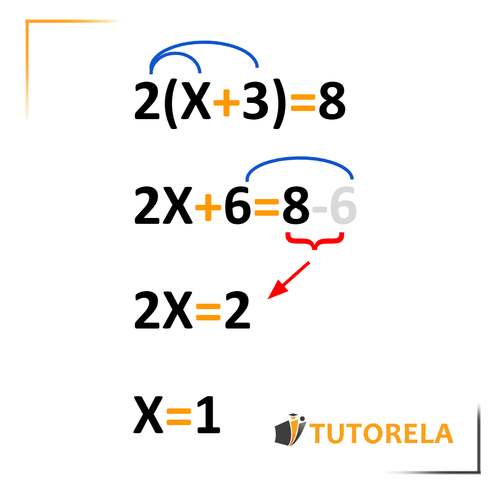
En esta ecuación, podemos ver claramente unos paréntesis. Para comenzar, debemos abrirlos (es decir, recurrir a la propiedad distributiva) y después podemos proseguir con las siguientes fases del ejercicio.
El resultado de la ecuación es .
Temas sugeridos para practicar con anticipación
Practicar Solución de una ecuación usando la propiedad distributiva
Halle el valor del parámetro x:
\( 7(-2x+5)=77 \)
Halle el valor del parámetro x:
\( 5(x+3)=0 \)
Halle el valor para el parámetro x:
\( -3(\frac{1}{2}x+4)=\frac{1}{2} \)
\( -6(7x-6)-(-5-8x)=0 \)
\( 5(8+a)-(2a+14)=56 \)
ejemplos con soluciones para Solución de una ecuación usando la propiedad distributiva
Ejercicio #1
Halle el valor del parámetro x:
Solución en video
Solución Paso a Paso
Para abrir paréntesis usaremos la fórmula:
Multiplicamos en consecuencia
Pasaremos el 35 hacia la sección de la derecha y cambiaremos el signo en consecuencia:
Resolvemos el ejercicio de resta del lado derecho y obtendremos:
Dividimos las dos secciones por -14
Respuesta
-3
Ejercicio #2
Halle el valor del parámetro x:
Solución en video
Solución Paso a Paso
Abrimos los paréntesis según la fórmula:
Pasaremos el 15 hacia la sección derecha y mantenemos el signo correspondiente:
Dividimos las dos secciones por 5
Respuesta
Ejercicio #3
Halle el valor para el parámetro x:
Solución en video
Solución Paso a Paso
Abrimos los paréntesis del lado izquierdo por la propiedad distributiva y usamos la fórmula:
Multiplicamos todos los términos por 2 para deshacernos de las fracciones:
Desplazaremos el menos 24 a la sección derecha y mantenemos el signo correspondiente:
Dividimos las dos secciones por menos 3:
Respuesta
Ejercicio #4
Solución en video
Solución Paso a Paso
Utilizamos la propiedad distributiva amplia y la fórmula:
Ingresamos los términos adecuados:
Desplazamos el menos 34x hacia el lado derecho y mantenemos el signo correspondiente:
Dividimos ambas secciones por 34:
Convertimos la fracción simple en una fracción mixta:
Respuesta
Ejercicio #5
Solución en video
Solución Paso a Paso
Abrimos los paréntesis por la propiedad distributiva y usamos la fórmula:
Sumamos los términos en consecuencia:
Desplazamos el 26 hacia el lado derecho y mantenemos el signo el correspondiente:
Dividimos ambos lados por 3:
Respuesta
Halle el valor del parámetro x:
\( -9(2-x)=(x+4)\cdot3 \)
Halle el valor del parámetro x:
\( -8(2x+4)=6(x-4)+3 \)
Halle el valor del parámetro x:
\( 8(x-2)=-4(x+3) \)
Halle el valor del parámetro x:
\( -7(2x+3)-4(x+2)=5(2-3x) \)
Halla el valor del parámetro x:
\( 2(4-x)=8 \)
Ejercicio #6
Halle el valor del parámetro x:
Solución en video
Solución Paso a Paso
Abrimos los paréntesis en ambas secciones por la propiedad distributiva y usamos la fórmula:
Desplazamos a 3X a la sección izquierda, y al 18 a la sección derecha y mantenemos los signos correspondientes:
Sumamos los términos:
Dividimos las dos secciones por 6:
Respuesta
5
Ejercicio #7
Halle el valor del parámetro x:
Solución en video
Solución Paso a Paso
Para abrir paréntesis usaremos la fórmula:
Multiplicamos en consecuencia:
Calcula los elementos en la sección derecha:
En la sección izquierda ingresamos los elementos con la X y en la sección izquierda los que no tienen la X, recuerde cambiar los signos más y menos según corresponda al transferir:
Calcula los elementos en consecuencia
Dividimos las dos secciones por 22
Respuesta
Ejercicio #8
Halle el valor del parámetro x:
Solución en video
Solución Paso a Paso
Para abrir paréntesis usaremos la fórmula:
Multiplicamos en consecuencia
En la sección izquierda ingresamos los elementos con la X y en la sección derecha los que no tienen la X, recuerde cambiar los signos más y menos según corresponda al transferir:
Resolvemos en consecuencia
Dividimos las dos secciones por 12
Reducimos y obtenemos
Respuesta
Ejercicio #9
Halle el valor del parámetro x:
Solución en video
Solución Paso a Paso
Para abrir paréntesis usaremos la fórmula:
Multiplicamos en consecuencia:
Calculamos los elementos en la sección izquierda:
En la sección izquierda ingresamos los elementos con la X y en la sección derecha los que no tienen la X, recuerde cambiar los signos más y menos según corresponda al transferir:
Calculamos los elementos en consecuencia:
Dividimos las dos secciones por -3:
Respuesta
-13
Ejercicio #10
Halla el valor del parámetro x:
Solución en video
Respuesta
0
\( 8a+2(3a-7)=0 \)
\( 3(a+1)-3=0 \)
\( 5-(3b-1)=0 \)
\( 3x+5(x+4)=0 \)
\( 2(x+4)+8=0 \)