Resolución de ecuaciones utilizando la propiedad distributiva

La resolución de una ecuación utilizando la propiedad distributiva está relacionada con la necesidad de abrir los paréntesis como primer paso para después poder simplificar los miembros similares. Cuando una ecuación contiene uno o más pares de paréntesis, debemos comenzar por abrirlos todos y después proseguir con la siguiente fase.

A continuación, te dejamos algunos ejemplos donde se aplica este método

$2\left(X+3\right)=8$

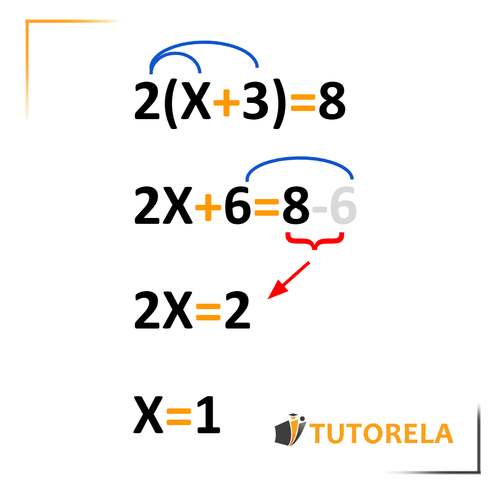
En esta ecuación, podemos ver claramente unos paréntesis. Para comenzar, debemos abrirlos (es decir, recurrir a la propiedad distributiva) y después podemos proseguir con las siguientes fases del ejercicio.

$2X+6=8$

$2X=2$

$X=1$

El resultado de la ecuación es $1$ .

Resolución de ecuaciones utilizando la propiedad distributiva

Explicación completa

Ir a prácticas

¡Pruébate en solución de una ecuación usando la propiedad distributiva!

Halle el valor del parámetro x:

$$ 5(x+3)=0 $$

Quiz y otros ejercicios

Otro ejemplo

$5\left(X+2\right)=3\left(X+4\right)$

En esta ecuación, vemos claramente que hay dos pares de paréntesis, uno en cada miembro. Para comenzar, debemos abrirlos (es decir, recurrir a la propiedad distributiva) y después podemos proseguir con las siguientes fases del ejercicio.

$5X+10=3X+12$

$2X=2$

$X=1$

El resultado de la ecuación es $1$ .

Si este artículo te interesó también te pueden interesar los siguientes artículos

En la página web de Tutorela encontrarás una gran variedad de artículos sobre matemáticas

Ejemplos y ejercicios con soluciones de resolución de ecuaciones utilizando la propiedad distributiva

Ejercicio #1

Halle el valor del parámetro x:

$5(x+3)=0$

Solución en video

Solución Paso a Paso

Abrimos los paréntesis según la fórmula:

$a(x+b)=ax+ab$

$5\times x+5\times3=0$

$5x+15=0$

Pasaremos el 15 hacia la sección derecha y mantenemos el signo correspondiente:

$5x=-15$

Dividimos las dos secciones por 5

$\frac{5x}{5}=\frac{-15}{5}$

$x=-3$

Respuesta

$-3$

Ejercicio #2

Halle el valor del parámetro x:

$7(-2x+5)=77$

Solución en video

Solución Paso a Paso

Para abrir paréntesis usaremos la fórmula:

$a(x+b)=ax+ab$

$(7\times-2x)+(7\times5)=77$

Multiplicamos en consecuencia

$-14x+35=77$

Pasaremos el 35 hacia la sección de la derecha y cambiaremos el signo en consecuencia:

$-14x=77-35$

Resolvemos el ejercicio de resta del lado derecho y obtendremos:

$-14x=42$

Dividimos las dos secciones por -14

$\frac{-14x}{-14}=\frac{42}{-14}$

$x=-3$

Respuesta

-3

Ejercicio #3

Halle el valor para el parámetro x:

$-3(\frac{1}{2}x+4)=\frac{1}{2}$

Solución en video

Solución Paso a Paso

Abrimos los paréntesis del lado izquierdo por la propiedad distributiva y usamos la fórmula:

$a(x+b)=ax+ab$

$-\frac{3}{2}x-12=\frac{1}{2}$

Multiplicamos todos los términos por 2 para deshacernos de las fracciones:

$-3x-12\times2=1$

$-3x-24=1$

Desplazaremos el menos 24 a la sección derecha y mantenemos el signo correspondiente:

$-3x=24+1$

$-3x=25$

Dividimos las dos secciones por menos 3:

$\frac{-3x}{-3}=\frac{25}{-3}$

$x=-\frac{25}{3}$

Respuesta

$-\frac{25}{3}$

Ejercicio #4

$-6(7x-6)-(-5-8x)=0$

Solución en video

Solución Paso a Paso

Utilizamos la propiedad distributiva amplia y la fórmula:

$a(x+b)=ax+ab$

$-42x+36+5+8x=0$

Ingresamos los términos adecuados:

$-34x+41=0$

Desplazamos el menos 34x hacia el lado derecho y mantenemos el signo correspondiente:

$41=34x$

Dividimos ambas secciones por 34:

$\frac{41}{34}=\frac{34x}{34}$

$\frac{41}{34}=x$

Convertimos la fracción simple en una fracción mixta:

$x=1\frac{7}{34}$

Respuesta

$1\frac{7}{34}$

Ejercicio #5

$5(8+a)-(2a+14)=56$

Solución en video

Solución Paso a Paso

Abrimos los paréntesis por la propiedad distributiva y usamos la fórmula:

$a(x+b)=ax+ab$

$40+5a-2a-14=56$

Sumamos los términos en consecuencia:

$26+3a=56$

Desplazamos el 26 hacia el lado derecho y mantenemos el signo el correspondiente:

$3a=56-26$

$3a=30$

Dividimos ambos lados por 3:

$\frac{3a}{3}=\frac{30}{3}$

$a=10$

Respuesta

$10$

¡Únete a 30,000 estudiantes destacados en matemáticas!

Práctica ilimitada, guía de expertos: mejora tus habilidades matemáticas hoy

Comprueba tu conocimiento

Ejercicio 1

Halla el valor del parámetro x:

$$ 2(4-x)=8 $$

Ejercicio 2

Halle el valor del parámetro x:

$$ 7(-2x+5)=77 $$

Ejercicio 3

$$ 3x+5(x+4)=0 $$

Preguntas de repaso

¿Qué es la propiedad distributiva?

La propiedad distributiva es una propiedad en donde esta involucrada tanto a la suma como a la multiplicación, es decir, un número está multiplicando a la suma de otros dos números, y gracias a esta propiedad la podemos distribuir y escribir de la siguiente manera:

$a\left(b+c\right)=ab+ac$

Veamos algunos ejemplos de cómo podemos aplicar esta ley

Ejemplo 1

$3\left(2+5\right)=3\left(2\right)+3\left(5\right)$

$3\left(7\right)=6+15$

$21=21$

Ejemplo 2

$7\left(4+6\right)=7\left(4\right)+7\left(6\right)$

$7\left(10\right)=28+42$

$70=70$

Ejemplo 3

$4\left(x+6\right)=4\left(x\right)+4\left(6\right)$

Como en este caso no podemos hacer la suma que está adentro del paréntesis porque no son términos semejantes entonces solo quedaría de la siguiente manera usando la propiedad distributiva

$4\left(x+6\right)=4x+24$

¿Cómo sería el proceso de despeje utilizando la propiedad distributiva?

Cuando en una ecuación nos aparecen signos de agrupación, en este caso paréntesis, para poder realizar un despeje y poder conocer el valor de la variable que necesitamos encontrar y más aun cuando la variable está adentro de ese paréntesis, lo primero que tenemos que hacer es aplicar la propiedad distributiva y posteriormente ya quitando los paréntesis con ese proceso ahora si procedemos a realizar los despejes necesarios para conocer el valor que se quiere.

Solución de ecuaciones aplicando la propiedad distributiva.

Ahora veamos como es el manejo algebraico con la propiedad distributiva en ecuaciones, haremos algunos ejemplos de solución de ecuaciones aplicando la propiedad.

Ejemplo 1

Consigna. Aplica la propiedad distributiva en la siguiente ecuación:

$3\left(x+2\right)=12$

Solución.

Podemos ver que hay paréntesis y no podemos sumar lo que esta adentro de ese paréntesis, por lo tanto debemos de aplicar la propiedad distributiva

$3\left(x+2\right)=12$

$3x+6=12$

Ahora procedemos a hacer los despejes necesarios para dejar a la variable solita de un lado del igual

$3x=12-6$

$3x=6$

Dividimos entre $3$

$x=\frac{6}{3}$

$x=2$

Respuesta

$x=2$

Ejemplo 2.

Consigna. Encuentra la solución a la siguiente ecuación:

$5\left(x+2\right)=3\left(x+4\right)$

Solución. En este caso tenemos paréntesis en ambos lados del igual, por lo tanto debemos de aplicar la propiedad distributiva en los dos lados:

$5\left(x+2\right)=3\left(x+4\right)$

$5x+10=3x+12$

Agrupamos términos semejantes, es decir, pasamos de un lado del igual a todas las variables y del otro lado a las constantes

$5x-3x=12-10$

$2x=2$

Dividimos entre $2$

$x=\frac{2}{2}$

$x=1$

Respuesta

$x=1$

Ejemplo 3.

Consigna. Resuelve la siguiente ecuación

$2\left(2x+6\right)=3x+8$

Solución. Aplicamos la propiedad distributiva

$2\left(2x+6\right)=3x+8$

$4x+12=3x+8$

Agrupamos

$4x-3x=8-12$

$x=-4$

Respuesta

$x=-4$

¿Sabes cuál es la respuesta?

Ejercicio 1

$$ 8a+2(3a-7)=0 $$

Ejercicio 2

$$ 3(a+1)-3=0 $$

Ejercicio 3

$$ 5-(3b-1)=0 $$

Ir a prácticas