Diremos que una función es decreciente cuando, a medida que crece el valor de la variable independiente , disminuye el valor de la función .
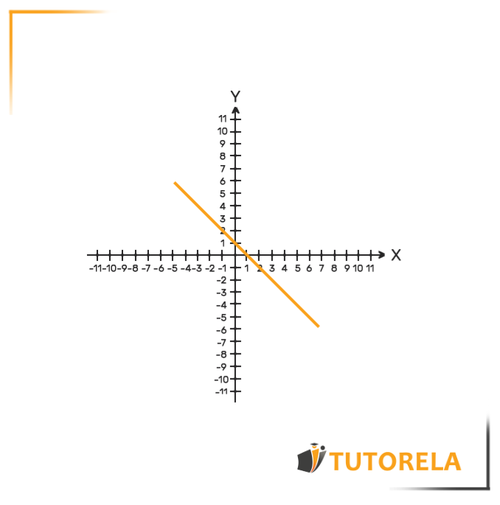
Diremos que una función es decreciente cuando, a medida que crece el valor de la variable independiente , disminuye el valor de la función .


¿En qué dominio la función aumenta?
Supongamos que tenemos dos elementos , a los que llamaremos y , donde se cumple lo siguiente: , es decir, está ubicado a la derecha de .
La función es decreciente cuando: y también .
La función puede ser decreciente en intervalos o en todo su dominio.

Si te interesa este artículo también te pueden interesar los siguientes artículos:
Representación gráfica de una función
Representación algebraica de una función
Asignación de valor numérico en una función
Intervalos de crecimiento y de decrecimiento de una función
En la página web de Tutorela encontrarás una variedad de artículos con interesantes explicaciones sobre matemáticas
Consigna
Halla el área decreciente de la función
Solución
coeficiente de
Por lo tanto
es el punto mínimo
El vértice de la función es
La función decrece en el área de
Respuesta
¿En qué dominio la función es negativa?
¿En qué dominio la función es ascendente?
¿En qué dominio la función crece?
Consigna
¿Cuándo la función es positiva?

Solución
El punto de corte con el eje es:
Antes positiva, luego negativa.
Por lo tanto
Respuesta
Consigna
Dada la función del diagrama, ¿cuál es su dominio de positividad?

Solución
Tenga en cuenta que toda la función siempre está por encima del eje:
Por lo tanto, siempre será positiva. Su área de positividad será para toda
Respuesta
Para toda
¿En qué intervalo la función es creciente?
Línea púrpura \( x=0.6 \)
¿La función en la gráfica disminuye en todo momento?
¿La función en la gráfica es decreciente?
Consigna
Dada la función del diagrama
¿Cuáles son las áreas de positividad y negatividad de la función?

Solución
Recordemos que una función es positiva cuando está arriba del eje y la función es negativa cuando se encuentra debajo del eje
Dado que el punto de intersección con el eje es
Cuando se encuentra por debajo de:
Cuando se encuentra por encima de:
Por lo tanto la función es positiva cuando y negativa cuando
Respuesta
Positivo cuando
Negativo cuando
Consigna
Halla el área creciente y decreciente de la función
Solución
En el primer paso tengamos en cuenta que
Por lo tanto y la parábola es el máximo
En el segundo paso halla a del vértice
según los datos que sabemos
Reemplazamos los datos en la fórmula
Luego sabemos que: y reemplazamos en la función y hallamos que
Respuesta
Decreciente
Creciente
¿La función mostrada en el gráfico a continuación es decreciente?
¿La función en el gráfico es decreciente?
¿La función en el gráfico de abajo es decreciente?
Determina qué dominio corresponde a la función descrita:
La función describe la cantidad de combustible en el tanque del automóvil según la distancia recorrida por el mismo.
Según la definición, la cantidad de combustible en el tanque del automóvil siempre disminuirá, ya que durante el viaje el automóvil consume combustible para desplazarse.
Por lo tanto, el dominio que es adecuado para esta función es - siempre decreciente.
Siempre decreciente
Elija la gráfica que mejor describa lo siguiente:
Aceleración de una pelota (Y) después de lanzarla desde un edificio en función del tiempo (X)
Dado que la aceleración depende del tiempo, será constante.
La fuerza de gravedad en la Tierra es constante, lo que significa que la velocidad de la gravedad terrestre es constante y, por lo tanto, el gráfico será recto.
El gráfico que aparece en la respuesta B satisface esto.
Elija la gráfica que mejor describa la siguiente historia:
Temperatura del agua tibia (Y) después de ponerla en el congelador en función del tiempo (X)
Dado que el punto de congelación del agua está por debajo de 0, la temperatura del agua debe descender por debajo de 0.
La gráfica en la respuesta B describe una función decreciente y, por lo tanto, esta es la respuesta correcta.
Determina si la función es creciente, decreciente o constante. Para cada función comprueba tus respuestas mediante un gráfico o una tabla.
Para cada número, multiplícalo por:
La función es:
Comencemos suponiendo que x es igual a 0:
Ahora supongamos que x es igual a menos 1:
Ahora supongamos que x es igual a 1:
Ahora supongamos que x es igual a 2:
Graficamos todos los puntos en la gráfica de la función:
Podemos ver que la función que obtuvimos es una función decreciente.
Decreciente
Determina si la función es creciente, decreciente o constante. Para cada función comprueba tus respuestas mediante un gráfico o una tabla.
Para cada número, multiplícalo por 0
La función es:
Comencemos suponiendo que x es igual a 0:
Ahora supongamos que x es igual a 1:
Ahora supongamos que x es igual a -1:
Ahora supongamos que x es igual a 2:
Graficamos todos los puntos en la gráfica de la función:
Podemos ver que la función que obtuvimos es una función constante.
Constante