En este artículo aprenderemos resumidamente todo lo necesario sobre los triángulos y además ¡practicaremos con algunos ejercicios!
¡Comencemos!
Ejercicios de Triángulos - Práctica Completa Online
Resuelve problemas de triángulos paso a paso: área, perímetro, ángulos, congruencia y semejanza. Practica con ejercicios interactivos y soluciones detalladas.
📚¡Domina los Triángulos con Práctica Interactiva!
- Calcula el área y perímetro de triángulos equiláteros, isósceles y escalenos
- Encuentra ángulos faltantes usando la propiedad de suma 180°
- Identifica y clasifica triángulos según sus lados y ángulos
- Aplica criterios de congruencia ALA, LAL, LLL y LLA
- Demuestra semejanza de triángulos usando teoremas AA y LLL
- Resuelve problemas reales con triángulos rectángulos y teorema de Pitágoras
Entendiendo la Triángulo
Explicación completa con ejemplos
Triángulo
Practicar Triángulo
Pon a prueba tus conocimientos con más de 37 cuestionarios
Dado el triángulo:
¿Cuál es su perímetro?
ejemplos con soluciones para Triángulo
Soluciones paso a paso incluidas
Ejercicio #1
Dado el triángulo ABC.
AC = 10 cm, AD = 3 cm, BC = 11.6 cm
¿Cuál es el área del triángulo?
Solución Paso a Paso
El triángulo que estamos viendo es el triángulo grande - ABC
El triángulo está formado por tres lados AB, BC y CA.
Ahora recordemos lo que necesitamos para el cálculo de un área triangular:
(lado x la altura que desciende del lado)/2
Por lo tanto, lo primero que debemos encontrar es una altura y un lado adecuados.
Se nos da el AC lateral, pero no hay altura que desciende, por lo que no nos sirve.
El lado AB no está dado,
Y así nos quedamos con el lado BC, que está dado.
Por el lado BC desciende la altura AD (los dos forman un ángulo de 90 grados).
Se puede argumentar que BC es también una altura, pero si profundizamos parece que CD puede ser una altura en el triángulo ADC,
y BD es una altura en el triángulo ADB (ambos son los lados de un triángulo rectángulo, por lo tanto son la altura y el lado).
Como no sabemos si el triángulo es isósceles o no, tampoco es posible saber si CD=DB, o cuál es su razón, y esta teoría falla.
Recordemos nuevamente la fórmula del área triangular y reemplacemos los datos que tenemos en la fórmula:
(lado* la altura que desciende del lado)/2
Ahora reemplazamos los datos existentes en esta fórmula:
Respuesta:
17.4
Solución en video
Ejercicio #2
Dados los tres ángulos:
Ángulo A es igual a 56°
Ángulo B es igual a 89°
Ángulo C es igual a 17°
¿Estos ángulos pueden componer un triángulo?
Solución Paso a Paso
Sumamos los tres ángulos para ver si son iguales a 180 grados:
La suma de los ángulos dados no es igual a 180, por lo que no pueden formar un triángulo.
Respuesta:
No
Solución en video
Ejercicio #3
Dados los tres ángulos:
Ángulo A es igual a 30°
Ángulo B es igual a 60°
Ángulo C es igual a 90°
¿Estos ángulos pueden componer un triángulo?
Solución Paso a Paso
Sumamos los tres ángulos para ver si son iguales a 180 grados:
La suma de los ángulos es igual a 180, por lo que pueden formar un triángulo.
Respuesta:
Si
Solución en video
Ejercicio #4
Dados los tres ángulos:
Ángulo A es igual a 90°
Ángulo B es igual a 115°
Ángulo C es igual a 35°
¿Estos ángulos pueden componer un triángulo?
Solución Paso a Paso
Sumamos los tres ángulos para ver si son iguales a 180 grados:
La suma de los ángulos dados no es igual a 180, por lo que no pueden formar un triángulo.
Respuesta:
No
Solución en video
Ejercicio #5
¿Cuál es el área del triángulo dado?
Solución Paso a Paso
Esta pregunta es un poco confusa, debido a que a partir de los datos necesitamos identificar cuáles son relevantes para nosotros y utilizar solo ellos.
Recordando la fórmula para el área de un triángulo:
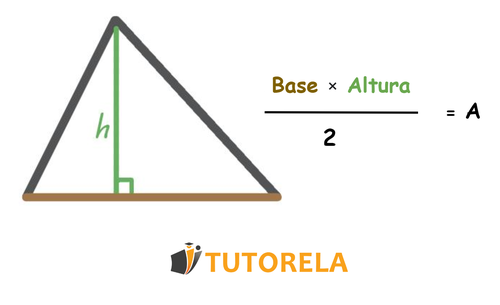Una altura es una línea recta que sale de un ángulo y forma un ángulo recto con el lado opuesto.
En el dibujo tenemos una altura, de longitud 6.
que baja hasta el lado rojo cuya longitud es 5.
Y por lo tanto, estos son los datos que utilizaremos.
Reemplazamos en la fórmula:
Respuesta:
15
Solución en video
Preguntas Frecuentes
¿Cómo calcular el área de un triángulo paso a paso?
+Para calcular el área de cualquier triángulo usa la fórmula: Área = (base × altura) ÷ 2. En triángulos rectángulos, usa: Área = (cateto₁ × cateto₂) ÷ 2. Siempre identifica primero qué tipo de triángulo tienes para aplicar la fórmula correcta.
¿Por qué la suma de ángulos de un triángulo siempre es 180°?
+Esta es una propiedad fundamental de la geometría euclidiana. Sin importar el tipo de triángulo (equilátero, isósceles, escaleno o rectángulo), sus tres ángulos internos siempre suman exactamente 180°. Esta regla te permite encontrar un ángulo desconocido si conoces los otros dos.
¿Cuál es la diferencia entre triángulos congruentes y semejantes?
+Los triángulos congruentes son idénticos en tamaño y forma (todos los lados y ángulos son iguales). Los triángulos semejantes tienen la misma forma pero diferente tamaño (ángulos iguales, lados proporcionales). La congruencia requiere igualdad exacta, la semejanza solo proporcionalidad.
¿Cómo identificar si un triángulo es equilátero, isósceles o escaleno?
+Observa los lados del triángulo:
• Equilátero: los 3 lados son iguales
• Isósceles: 2 lados son iguales
• Escaleno: los 3 lados son diferentes
También puedes identificarlos por sus ángulos: equilátero tiene tres ángulos de 60°, isósceles tiene dos ángulos base iguales.
¿Qué criterios puedo usar para demostrar congruencia de triángulos?
+Existen cuatro criterios principales:
1. LLL (Lado-Lado-Lado): tres lados iguales
2. LAL (Lado-Ángulo-Lado): dos lados y el ángulo entre ellos iguales
3. ALA (Ángulo-Lado-Ángulo): dos ángulos y el lado entre ellos iguales
4. LLA (Lado-Lado-Ángulo): dos lados y el ángulo opuesto al mayor
¿Cómo calcular el perímetro de diferentes tipos de triángulos?
+El perímetro siempre es la suma de los tres lados:
• Triángulo equilátero: P = 3 × lado
• Triángulo isósceles: P = 2 × lado_igual + base
• Triángulo escaleno: P = lado₁ + lado₂ + lado₃
• Triángulo rectángulo: P = cateto₁ + cateto₂ + hipotenusa
¿Qué es la altura, mediana y bisectriz de un triángulo?
+Son líneas especiales dentro del triángulo: La altura es perpendicular desde un vértice al lado opuesto. La mediana conecta un vértice con el punto medio del lado opuesto. La bisectriz divide un ángulo en dos partes iguales. En triángulos equiláteros, estas tres líneas coinciden.
¿Cómo resolver problemas de triángulos rectángulos?
+En triángulos rectángulos usa:
1. Teorema de Pitágoras: a² + b² = c² (donde c es la hipotenusa)
2. Para el área: (cateto₁ × cateto₂) ÷ 2
3. Funciones trigonométricas para encontrar ángulos
4. La suma de los dos ángulos agudos siempre es 90°