Ejercicios Área del Cuadrado: Problemas y Práctica Guiada

Esta pregunta es un poco confusa, debido a que a partir de los datos necesitamos identificar cuáles son relevantes para nosotros y utilizar solo ellos.

Recordando la fórmula para el área de un triángulo:

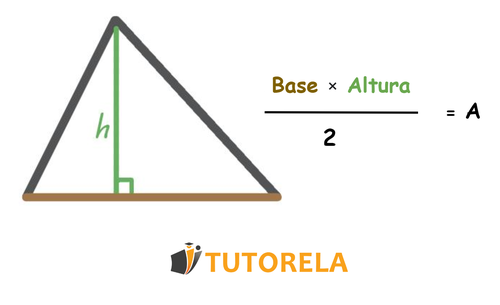Una altura es una línea recta que sale de un ángulo y forma un ángulo recto con el lado opuesto.

En el dibujo tenemos una altura, de longitud 6.

que baja hasta el lado rojo cuya longitud es 5.

Y por lo tanto, estos son los datos que utilizaremos.

Reemplazamos en la fórmula:

$\frac{6\times5}{2}=\frac{30}{2}=15$

Primero identificaremos las partes que necesitamos para poder hallar el área del triángulo.

Fórmula del área del triángulo: altura*lado al que desciende de la altura / 2

Como es un triángulo rectángulo, sabemos que los lados rectos en realidad también son las alturas entre sí, es decir, el lado que mide 5 y el lado que mide 7.

Multiplicamos los catetos y se divide por 2

$\frac{5\times7}{2}=\frac{35}{2}=17.5$

El triángulo que estamos viendo es el triángulo grande - ABC

El triángulo está formado por tres lados AB, BC y CA.

Ahora recordemos lo que necesitamos para el cálculo de un área triangular:

(lado x la altura que desciende del lado)/2

Por lo tanto, lo primero que debemos encontrar es una altura y un lado adecuados.

Se nos da el AC lateral, pero no hay altura que desciende, por lo que no nos sirve.

El lado AB no está dado,

Y así nos quedamos con el lado BC, que está dado.

Por el lado BC desciende la altura AD (los dos forman un ángulo de 90 grados).

Se puede argumentar que BC es también una altura, pero si profundizamos parece que CD puede ser una altura en el triángulo ADC,

y BD es una altura en el triángulo ADB (ambos son los lados de un triángulo rectángulo, por lo tanto son la altura y el lado).

Como no sabemos si el triángulo es isósceles o no, tampoco es posible saber si CD=DB, o cuál es su razón, y esta teoría falla.

Recordemos nuevamente la fórmula del área triangular y reemplacemos los datos que tenemos en la fórmula:

(lado* la altura que desciende del lado)/2

Ahora reemplazamos los datos existentes en esta fórmula:

$\frac{CB\times AD}{2}$

$\frac{11.6\times3}{2}$

$\frac{34.8}{2}=17.4$

Para calcular el área del rectángulo, multiplicamos el largo por el ancho:

$15\times3=45$

Usamos la fórmula (base+base) multiplicado por la altura y dividido por 2.

Tenga en cuenta que solo se nos proporciona una base y no es posible determinar el tamaño de la otra base.

Por lo tanto, no se puede calcular el área.