Ejemplos, ejercicios y soluciones de propiedad distributiva con ampliación

$(2x-3)\times(5x-7)$

Para responder a este ejercicio, necesitamos entender cómo funciona la propiedad distributiva extendida:

Por ejemplo:

(a+1)∗(b+2)

Para resolver este tipo de ejercicios se deben resolver los siguientes pasos:

Paso 1: multiplicamos el primer factor del primer paréntesis por cada uno de los factores del segundo paréntesis.

Paso 2: multiplicamos el segundo factor del primer paréntesis por cada uno de los factores del segundo paréntesis.

Paso 3: agrupamos en términos semejantes.

ab∗2a∗b∗2

Comenzamos desde el primer número del ejercicio: 2x

2x*5x+2x*-7

10x²-14x

Continuaremos con el segundo factor: -3

-3*5x+-3*-7

-15x+21

Sumamos todos los datos juntos:

10x²-14x-15x+21

10x²-29x+21

$10x^2-29x+21$

$(a+4)(c+3)=$

Cuando nos encontramos con un ejercicio de multiplicación de este tipo, podemos reconocer que se debe seguir la propiedad distributiva.

Paso 1: multiplica el primer factor del primer paréntesis por cada uno de los factores del segundo paréntesis.

Paso 2: multiplica el segundo factor del primer paréntesis por cada uno de los factores del segundo paréntesis.

Paso 3: agrupamos términos semejantes.

a * (c+3) =

a*c + a*3

4  * (c+3) =

4*c + 4*3

ac+3a+4c+12

No hay términos semejantes para simplificar aquí, ¡así que esta es la solución!

$ac+3a+4c+12$

¿Es posible utilizar la propiedad distributiva para simplificar la expresión dada

$(ab)(c d)$?

Recordemos la propiedad distributiva extendida:

$(\textcolor{red}{a}+\textcolor{blue}{b})(c+d)=\textcolor{red}{a}c+\textcolor{red}{a}d+\textcolor{blue}{b}c+\textcolor{blue}{b}d$Tengamos en cuenta que la operación entre los términos de la expresión dentro del paréntesis entre los cuales se realiza la multiplicación es una operación de multiplicación:

$(a b)(c d)$Esto contrasta con la operación entre los términos en las expresiones entre paréntesis en la propiedad distributiva ampliada antes mencionada, que es la suma (o la resta, que en realidad es la suma del término con un signo menos),

Además, notaremos que como hay una multiplicación entre todos los términos, tanto en la expresión dentro del paréntesis como entre las expresiones dentro del paréntesis, existe una multiplicación donde los paréntesis en realidad son redundantes y se pueden omitir y obtenemos:

\( (a b)(c d)= \\ abcd \)Por lo tanto, la apertura de los paréntesis en la expresión dada con el uso de la propiedad distributiva extendida es incorrecta y produce un resultado incorrecto.

Por lo tanto, la respuesta correcta es la opción d.

No, $abcd$

Una las expresiones de igual valor

1. $(a-b)(c-4)$

2. $(a+b)(c+4)$

3. $(a-b)(c+4)$

4. $(a+b)(c-4)$

   a.$ac-4a+bc-4b$

   b.$ac+4a-bc-4b$

   c.$ac-4a-bc+4b$

   d.$ac+4a+bc+4b$

Usamos todos los ejercicios de la propiedad distributiva extendida:$(a+b)\times(c+d)=ac+ad+bc+bd$

1.$(a-b)(c-4)=ac-4a-bc+4b$

2.$(a+b)(c+4)=ac+4a+bc+4b$

3.$(a-b)(c+4)=ac+4a-bc-4b$

4.$(a+b)(c-4)=ac-4a+bc-4b$

1-c, 2-d, 3-b, 4-a

¿Las expresiones de ambos lados son equivalentes?

$a^2+9a-20\stackrel{?}{=}(a+4)(a-5)$

Resolvemos el lado derecho de la ecuación usando la propiedad distributiva extendida:$(a+b)\times(c+d)=ac+ad+bc+bd$

$(a+4)(a-5)=a^2-5a+4a-20$

$a^2-a-20$

Es decir, la respuesta D es la correcta.

No, $-a$ en lugar de $+9a$

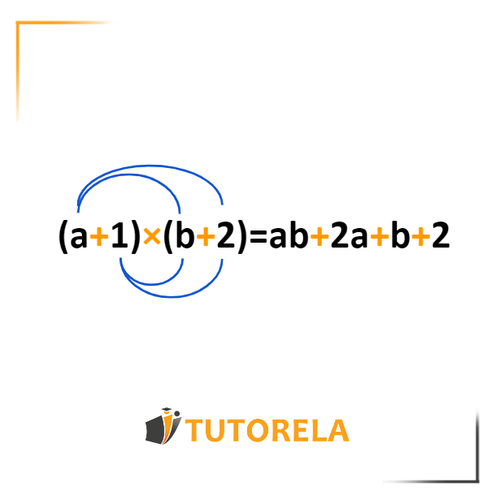
Simplifica la expresión dada:$(a+c)(4+c)$

Simplificamos la expresión dada, abrimos paréntesis usando la propiedad distributiva extendida:

$(\textcolor{red}{x}+\textcolor{blue}{y})(t+d)=\textcolor{red}{x}t+\textcolor{red}{x}d+\textcolor{blue}{y}t+\textcolor{blue}{y}d$Tengamos en cuenta que en la forma de la fórmula de la propiedad distributiva mencionada anteriormente, asumimos por defecto que la operación entre los términos dentro del paréntesis es una operación de suma, por lo tanto, por supuesto, no olvidaremos que el signo del coeficiente del término es parte inseparable de él, también aplicaremos las reglas de multiplicación de signos y así podremos presentar cualquier expresión entre paréntesis, que se abre mediante la fórmula anterior, primero, como una expresión en la que hay una operación de suma entre todos los términos, en esta expresión, como queda claro, para todos los términos el coeficiente es el signo más, por lo tanto vamos directamente a la apertura del paréntesis,

$$Comenzamos con la apertura de paréntesis:

\( (\textcolor{red}{x}+\textcolor{blue}{c})(4+c)\\ \textcolor{red}{x}\cdot 4+\textcolor{red}{x}\cdot c+\textcolor{blue}{c}\cdot 4+\textcolor{blue}{c} \cdot c\\ 4x+xc+4c+c^2 \)Para simplificar la expresión anterior, utilizamos la ley de potencias para la multiplicación entre términos con bases idénticas:

$a^m\cdot a^n=a^{m+n}$

En el siguiente paso entran términos semejantes, definiremos términos semejantes como términos en los que las incógnitas(cada una por separado), en este caso, x y c, tienen potencias idénticas (en ausencia de una de las incógnitas de la expresión , nos referiremos a su potencia como potencia de cero, esto se debe a que elevando cada número a la potencia de cero da como resultado 1), además usaremos la propiedad sustitutiva, además ordenaremos la expresión de mayor a la potencia más baja de izquierda a derecha (nos referiremos al número libre como la potencia de cero),

Tengamos en cuenta que en la expresión que obtuvimos en el último paso hay cuatro términos diferentes, esto se debe a que no hay ni siquiera un par de términos en los que las incógnitas (diferentes) tengan la misma potencia, además ya está ordenado según potencia como arriba, por lo tanto la expresión que ya hemos obtenido es la expresión final y más simplificada:\( \textcolor{purple}{4x}\textcolor{green}{+xc}\textcolor{black}{+4c}\textcolor{orange}{+c^2 }\\ \textcolor{orange}{c^2 }\textcolor{green}{+xc}\textcolor{purple}{+4x}\textcolor{black}{+4c}\\ \)Resaltamos a los diferentes términos mediante colores y, como se enfatizó antes, nos aseguramos de que el signo principal del término sea una parte integral del mismo.

Utilizamos la propiedad sustitutiva por la multiplicación para notar que la respuesta correcta es la opción A.

$4x+cx+4c+c^2$

Es posible utilizar la propiedad distributiva para simplificar la expresión

$(17+c)(5+a+3)$

Podemos utilizar el paréntesis de la derecha ya que se puede simplificar de la siguiente manera:

(8+a)

Luego obtendremos el ejercicio:

$(17+c)(8+a)=$

$136+17a+8c+ca$

Si, $136+17a+8c+ca$

Una las expresiones (en números) con las expresiones equivalentes (en letras):

1. $(2x-y)(x+3)$

2. $(y-2x)(3-x)$

3. $(2x+y)(x-3)$

   a.$2x^2-6x+yx-3y$

   b.$2x^2-6x-yx+3y$

   c.$2x^2+6x-yx-3y$

Simplifica las expresiones dadas, abra paréntesis usando la propiedad distributiva extendida:

$(\textcolor{red}{a}+\textcolor{blue}{b})(c+d)=\textcolor{red}{a}c+\textcolor{red}{a}d+\textcolor{blue}{b}c+\textcolor{blue}{b}d$Tengamos en cuenta que en la forma de la fórmula para la propiedad distributiva mencionada anteriormente, asumimos por defecto que la operación entre los términos dentro del paréntesis es una suma, por lo tanto , por supuesto, no olvidaremos que el signo del coeficiente del término es un parte inseparable de él. Además, aplicaremos las reglas de multiplicación de signos y así podremos presentar cualquier expresión entre paréntesis, que se abre con la ayuda de la fórmula anterior, primero, como una expresión en la que tiene lugar una operación de suma entre todos los términos (si es necesario),

Luego simplificaremos todas y cada una de las expresiones del problema dado, respetando lo anterior, primero abriremos los paréntesis mediante la propiedad distributiva mencionada anteriormente. Luego usaremos la propiedad sustitutiva en la suma y multiplicación, e introduciremos términos semejantes (si hay términos semejantes en la expresión obtenida después de abrir los paréntesis):

1. \( (2x-y)(x+3) \\ \downarrow\\ \big(2x+(-y)\big)(x+3) \\ 2x\cdot x+2x\cdot 3+(-y)\cdot x+(-y)\cdot3\\ \boxed{2x^2+6x-yx-3y}\\ \)

2. \( (y-2x)(3-x) \\ \downarrow\\ \big(y+(-2x)\big)\big(3+(-x)\big) \\ y\cdot 3+y\cdot (-x)+(-2x)\cdot 3+(-2x)\cdot(-x)\\ \boxed{3y-xy-6x+2x^2}\\ \)

3. \( (2x+y)(x-3) \\ \downarrow\\ (2x+y)(x+(-3)) \\ 2x\cdot x+2x\cdot (-3)+y\cdot x+y\cdot(-3)\\ \boxed{2x^2-6x+yx-3y}\\ \)Como puedes notar, en todas las expresiones en las que aplicamos la multiplicación entre las expresiones en los paréntesis anteriores, el resultado de la multiplicación (obtenido luego de aplicar la propiedad distributiva antes mencionada) produjo una expresión en la que no se pueden sumar términos, y esto es porque todos los términos en la expresión resultante son diferentes entre sí (recuerde que todas las incógnitas semejantes deben ser idénticas y estar en la misma potencia),

   Ahora, usemos la propiedad sustitutiva en la suma y la multiplicación para distinguir que:

   La expresión simplificada en 1 corresponde a la expresión en la opción C,

   La expresión simplificada en 2 corresponde a la expresión de la opción B,

   La expresión simplificada en 3 corresponde a la expresión de la opción A,

Por lo tanto, la respuesta correcta (entre las opciones que se ofrecen) es la opción B.

1-c, 2-b, 3-a

Simplifica la expresión

$(3a-4)b+2$

Simplificamos la expresión, abrimos los paréntesis mediante la propiedad distributiva:

$x(y+z)=xy+xz$Tengamos en cuenta que en la forma de la fórmula de la propiedad distributiva mencionada anteriormente asumimos por defecto que la operación entre los términos dentro del paréntesis es una operación suma, por lo tanto, por supuesto, no olvidaremos que el signo del coeficiente del término es inseparable de él. Además, aplicamos las reglas de multiplicación de signos y así podemos presentar cualquier expresión entre paréntesis, que se abre con la ayuda de la fórmula anterior, primero, como una expresión en la que hay una operación de suma entre todos los términos:

\( (3a-4)b+2\\ \big(3a+(-4)\big)b+2 \)Continuamos y abrimos los paréntesis usando la propiedad distributiva:

\( \big(3a+(-4)\big)b+2\\ 3a\cdot b+(-4)\cdot b +2\\ 3ab-4b+2 \)Por lo tanto, la respuesta correcta es la opción c.

$3ab-4b+2$