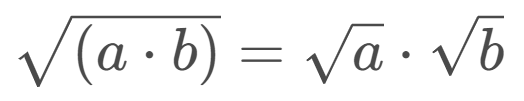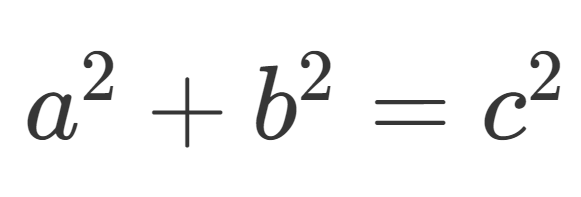Ejercicios del Teorema de Pitágoras - Práctica con Soluciones

Domina el Teorema de Pitágoras con ejercicios paso a paso. Aprende a calcular hipotenusa y catetos en triángulos rectángulos con ejemplos resueltos.

📚¿Qué aprenderás practicando el Teorema de Pitágoras?

Calcular la hipotenusa conociendo los dos catetos del triángulo rectángulo
Encontrar un cateto cuando conoces la hipotenusa y el otro cateto
Resolver problemas de triángulos isósceles usando el Teorema de Pitágoras
Aplicar el teorema inverso para determinar si un triángulo es rectángulo
Solucionar ejercicios con raíces cuadradas y operaciones algebraicas
Resolver problemas de la vida real con rampas, escaleras y distancias

Entendiendo la Teorema de Pitágoras

Explicación completa con ejemplos

Que dice el teorema de pitagoras

El Teorema de Pitágoras se puede formular de la siguiente manera: en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos

En el triángulo rectángulo que se muestra en la imágen a continuación usamos las primeras letras del alfabeto para designar sus lados:

$a$ y $b$ son los catetos

$c$ es la hipotenusa

Podemos ahora expresar el teorema de Pitágoras en forma algebraica del siguiente modo:

$c²=a²+b²$

Podemos expresar en forma geométrica el Teorema de Pitagoras a través de la siguiente imagen, donde se puede demostrar que el area del cuadrado $c$ ) (cuadrado de la hipotenusa) es la suma de las areas de los cuadrados ( $a$ ) y ( $b$ ) (cuadrados de los catetos).

Explicación completa

Practicar Teorema de Pitágoras

Pon a prueba tus conocimientos con más de 40 cuestionarios

En el rectángulo ABCD dado:

$$ BD=25,BC=7 $$

Calcula el área del rectángulo.

ejemplos con soluciones para Teorema de Pitágoras

Soluciones paso a paso incluidas

Ejercicio #1

Considera un triángulo rectángulo, AB = 8 cm y AC = 6 cm.
Calcula la longitud del lado BC.

Solución Paso a Paso

Para encontrar la longitud de la hipotenusa BC en un triángulo rectángulo donde AB y AC son los otros dos lados, usamos el teorema de Pitágoras: $c^2 = a^2 + b^2$ .

Aquí, $a = 6 \text{ cm}$ y $b = 8 \text{ cm}$ .

Sustituyendo los valores en el teorema de Pitágoras, obtenemos:

$c^2 = 6^2 + 8^2$ .

Calculando:

$c^2 = 36 + 64$

$c^2 = 100$ .

Tomando la raíz cuadrada de ambos lados:

$c = 10 \text{ cm}$ .

Respuesta:

10 cm

Ejercicio #2

Dado el triángulo del dibujo. ¿Cuál es el largo AB?

Solución Paso a Paso

Para hallar el lado AB, necesitaremos usar el teorema de Pitágoras.

El teorema de Pitágoras nos permite hallar el tercer lado de un triángulo rectángulo, si tenemos los otros dos lados.

Puedes leer todo sobre el teorema aquí.

Teorema de Pitágoras:

$A^2+B^2=C^2$

Es decir, un lado de un cuadrado más el segundo lado de un cuadrado es igual al tercer lado de un cuadrado.

Reemplazamos los datos existentes:

$3^2+2^2=AB^2$

$9+4=AB^2$

$13=AB^2$

Extraemos la raíz:

$\sqrt{13}=AB$

Respuesta:

$\sqrt{13}$ cm

Solución en video

Ejercicio #3

Dado el triángulo del dibujo. Halla el largo AC

Solución Paso a Paso

Para resolver el ejercicio, tenemos que utilizar el teorema de Pitágoras:

A²+B²=C²

Reemplazamos los datos que tenemos:

3²+4²=C²

9+16=C²

25=C²

5=C

Respuesta:

5 cm

Solución en video

Ejercicio #4

Dado el triángulo rectángulo:

¿Cuál es el largo del tercer lado?

Solución Paso a Paso

Usamos el teorema de Pitágoras

$AC^2+AB^2=BC^2$

Reemplazamos los datos que conocemos:

$3^2+4^2=BC^2$

$9+16=BC^2$

$25=BC^2$

Extraemos la raíz:

$\sqrt{25}=BC$

$5=BC$

Respuesta:

Solución en video

Ejercicio #5

Dado el triángulo:

¿Cuál es el valor de X?

Solución Paso a Paso

Es importante recordar: el teorema de Pitágoras es válido solo para triángulos rectángulos.

Este triángulo no tiene un ángulo recto y, por lo tanto, el lado que falta no se puede calcular de esta manera.

Respuesta:

No se puede resolver

Solución en video

Preguntas Frecuentes

Todo lo que necesitas saber Teorema de Pitágoras

¿Cómo se calcula la hipotenusa en el Teorema de Pitágoras?

Para calcular la hipotenusa, usa la fórmula c² = a² + b², donde c es la hipotenusa y a, b son los catetos. Suma los cuadrados de los catetos y extrae la raíz cuadrada del resultado.

¿Cuándo se puede usar el Teorema de Pitágoras?

El Teorema de Pitágoras solo se aplica en triángulos rectángulos, es decir, triángulos que tienen un ángulo de 90 grados. No funciona en triángulos obtusos o agudos.

¿Cómo encuentro un cateto conociendo la hipotenusa?

Para encontrar un cateto, despeja de la fórmula: a² = c² - b². Resta el cuadrado del cateto conocido del cuadrado de la hipotenusa, luego extrae la raíz cuadrada.

¿Qué es el teorema inverso de Pitágoras?

El teorema inverso establece que si a² + b² = c² en un triángulo, entonces ese triángulo es rectángulo. Se usa para verificar si un triángulo tiene un ángulo de 90 grados.

¿Cómo resolver ejercicios de Pitágoras paso a paso?

1. Identifica si el triángulo es rectángulo 2. Determina qué lado es la hipotenusa (el más largo) 3. Aplica la fórmula c² = a² + b² 4. Sustituye los valores conocidos 5. Despeja la incógnita y calcula la raíz cuadrada

¿Se puede usar Pitágoras en triángulos isósceles?

Sí, cuando trazas la altura desde el vértice hasta la base, divides el triángulo isósceles en dos triángulos rectángulos congruentes. Entonces puedes aplicar el Teorema de Pitágoras a cada uno.

¿Qué hacer si el resultado tiene raíz cuadrada?

Si el resultado no es un número entero perfecto, como √50, puedes simplificarlo (√50 = 5√2) o usar una calculadora para obtener el valor decimal aproximado (7.07).

¿Para qué sirve el Teorema de Pitágoras en la vida real?

Se usa para calcular distancias, como la longitud de escaleras, rampas, cables de tensión, o para encontrar la distancia más corta entre dos puntos. Es fundamental en construcción, arquitectura y navegación.

Practica por Tipo de Pregunta

Elige tu estilo de aprendizaje y formato de práctica preferido para problemas de fracciones

Aplicación de la fórmula Cálculo usando la diagonal Dos triángulos El perímetro de un triángulo En combinación con el área del triángulo Problemas de espacio y movimiento matemáticos Problemas escritos Triángulo isósceles Usando formas geométricas adicionales Uso del Teorema de Pitágoras Uso de proporciones para el cálculo Uso de variables Uso inverso del teorema

Más Recursos y Enlaces

Explora más recursos y enlaces relacionados con Teorema de Pitágoras

Practicar La aplicación del teorema de Pitágoras en un ortoedro o cuboide Practicar Congruencia de triángulos rectángulos (en el contexto del Teorema de Pitágoras)