Figuras tridimensionales

¿Qué son las figuras tridimensionales?

Hasta ahora hemos trabajado con figuras bidimensionales comunes como, por ejemplo, el cuadrado o el triángulo.
Las figuras tridimensionales son aquellas que se extienden a la tercera dimensión, es decir, que además de longitud y anchura también tienen altura (o sea, la figura tiene profundidad).

¿Qué diferencia tienen las figuras tridimensionales?

Las figuras tridimensionales cuentan con varias definiciones que enseguida veremos:
A continuación hay una figura tridimensional que usaremos para aprender cada definición - El cubo:

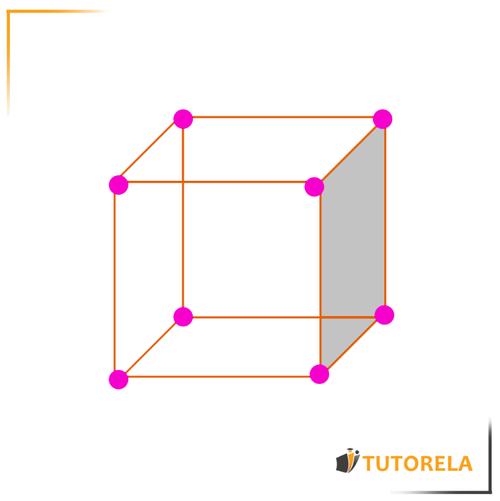
Cara: es el lado plano de una figura tridimensional
En el cubo que tenemos aquí hay 6 caras (una de ellas está pintada de color gris)
Borde: son las aristas que unen una cara con la otra en una figura tridimensional
En el cubo que tenemos aquí hay 12 bordes (pintados de verde)
Vértice: es el punto que une los bordes
En el cubo que tenemos aquí hay 8 vértices (pintados de anaranjado)

Volumen: es la cantidad de espacio contenido dentro de una figura tridimensional.
Las unidades de medida son $cm^3$ .

Ortoedro

El ortoedro es una figura tridimensional compuesta por 6 rectángulos.

Cada ortoedro tiene:

6 caras: los rectángulos que componen el ortoedro - tres pares de rectángulos que pueden ser diferentes unos de otros.
12 Bordes: las aristas del ortoedro (se dividen en largo, ancho y altura) - marcados con verde
8 Vértices: los puntos que unen las aristas - marcadas con anaranjado

Puedes profundizar sobre las partes del ortoedro leyendo este artículo

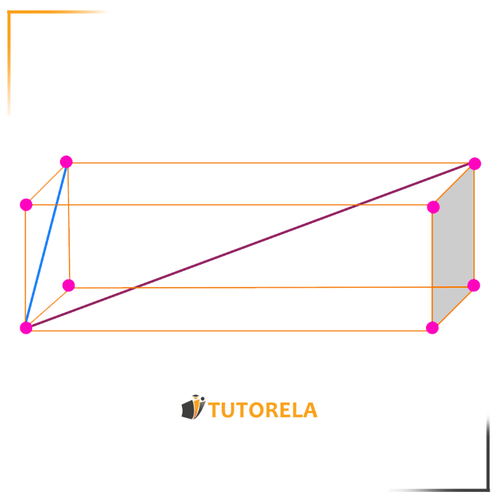
Diagonales de la cara:

Las diagonales que van de un vértice a otro de la misma cara siempre y cuando que los vértices pertenezcan a la misma cara - marcado con azul

Diagonal del ortoedro:

Las diagonales que van de un vértice a otro sobre caras diferentes, siempre y cuando que los 2 vértices pertenezcan a la misma cara - marcado con rojo

Volumen del ortoedro

El volumen del ortoedro es ( \times \~la~anchura~\times \~la~longitud\la~altura\)

Para más información sobre el volumen del ortoedro haz clic aquí

¡Únete a 30,000 estudiantes destacados en matemáticas!

Práctica ilimitada, guía de expertos: mejora tus habilidades matemáticas hoy

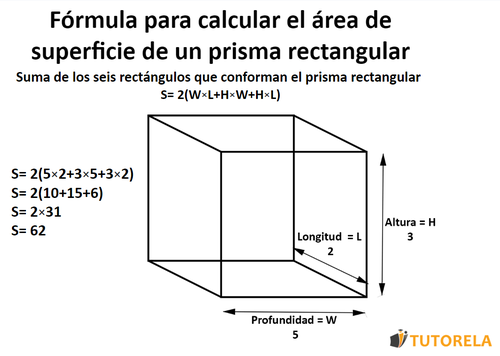
Superficie de un ortoedro

La fórmula para sacar el área de superficiees(anchura\times \longitud + altura\times \anchura+ altura\times \longitud)\times \2

Puedes volver a leer sobre el área de un ortoedro haciendo clic aquí

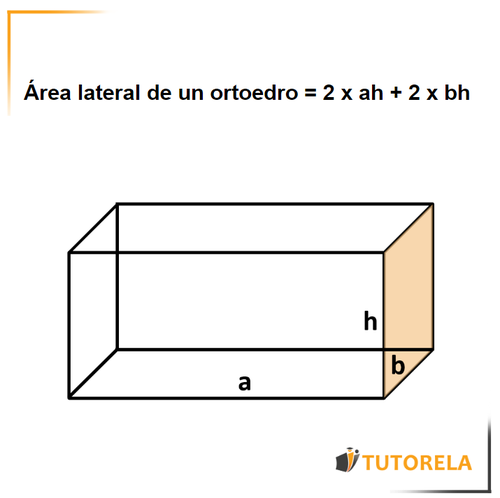
Área lateral de un ortoedro

Es la suma del área de los cuatro rectángulos laterales (sin las bases).
Se puede calcular el área lateral de un ortoedro con la siguiente fórmula:
a- Longitud
b- Anchura
h- Altura

2\times \ah+2\times \bh= área~de~un~ortoedro\lateral

Puedes volver a leer sobre el área lateral de un ortoedro haciendo clic aquí
Para más información sobre el ortoedro haz clic aquí

Cilindro

El cilindro es una figura tridimensional compuesta por dos círculos idénticos paralelos denominados bases, entre los cuales se expande el área lateral.

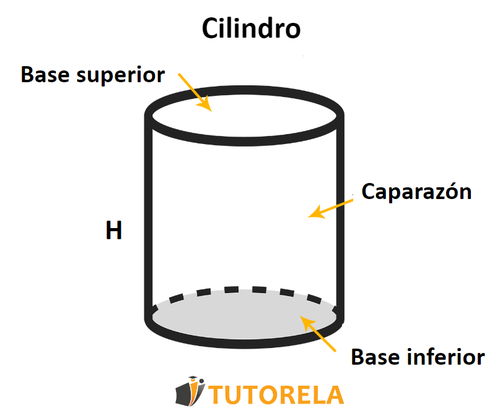
Otras propiedades:

La distancia entre las dos bases es constante y se llama altura del cilindro - la marcaremos con una $H$
El radio de ambas bases es igual, lo marcaremos con una $R$

Volumen del cilindro

Al volumen contenido dentro del cilindro se acostumbra a marcarlo con $V$ .
Fórmula para calcular el volumen del cilindro:
$π\times \R^2\times \H = V$

Cuando:

$π$ = PI ( $3.14$ )
$R$ = Radio de la base
$H$ = Altura del cilindro

Para más información sobre el volumen del cilindro haz clic aquí

Superficie total del cilindro de un cilindro

El total del área lateral y las dos bases - lo señalaremos con $A$
Utilizaremos la fórmula:

$2πR\times \H+2π\times \R^2$

Superficie total del cilindro de un cilindro

Cuando:

$π$ = PI ( $3.14$ )
$R$ = Radio de la base
$H$ = Altura del cilindro

Para más información haz clic aquí

Área lateral de un cilindro

Sólo el área lateral sin las bases. Lo señalaremos con $S$
Utilizaremos la fórmula:

2πR\times \H

Cuando:

$π$ = PI ( $3.14$ )
$R$ = Radio de la base
$H$ = Altura del cilindro

Para más información sobre el cilindro haz clic aquí

Prisma

El prisma triangular recto es una figura tridimensional que está compuesta por 2 triángulos y 3 rectángulos:

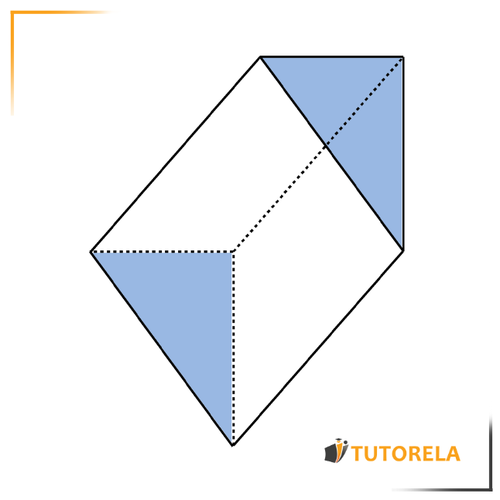
Base del prisma: los 2 triángulos que lo componen siempre serán idénticos (marcados con anaranjado).
Los triángulos pueden ser isósceles, escalenos o equiláteros.
Para profundizar sobre el tema de las bases del prisma haz clic aquí
Caras del prisma: los 3 rectángulos que conforman las caras laterales - no necesariamente serán idénticas.
Alturas del prisma: las tres rectas que unen las bases - siempre tiene el mismo largo.
Para más información sobre las alturas del prisma haz clic aquí

¡Practiquemos!
¿En un prisma triangular recto las bases triangulares siempre son idénticas?
Solución:
¡Sí! Los triángulos, que de hecho son las bases, siempre son iguales.
Ejercicio:
¿Cuántas alturas hay en un prisma triangular recto?
¿Son idénticas?
Solución:
Hay 3 alturas en un prisma triangular recto y siempre tienen el mismo largo.
Ejercicio:
¿Los tres rectángulos que componen las caras laterales del prisma deben ser idénticos?
Solución:
No.
Las aristas del triángulo no deben ser iguales necesariamente y esto podría crear rectángulos diferentes.

Volumen del prisma triangular recto

Se suele expresar el volumen del prisma a través de la siguiente fórmula:
$V= S \cdot H$

$S$ = Área de la base
$H$ = Altura del prisma

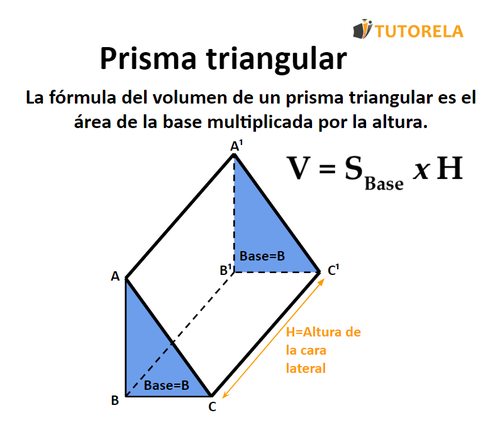
Puedes volver a leer sobre el área del prisma haciendo clic aquí

Área de un prisma triangular recto

El área de un prisma triangular recto es, de hecho, la suma total de las superficies de sus dos bases (los triángulos) y de sus tres caras laterales (los rectángulos).

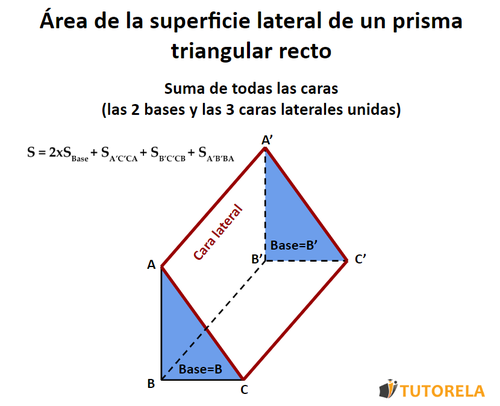
Área de la superficie lateral de un prisma triangular recto

Para más información sobre el área del prisma haz clic aquí