División y línea de fracción

Cuando estudiamos el orden de las operaciones matemáticas nos encontramos con los términos división y línea de fracción, pero ¿qué quiere decir esto y por qué es tan especial? 

En primer lugar, debemos recordar que la línea de fracción es exactamente lo mismo que una división. 10:2 es igual a ${\ {10 \over 2}}$ y exactamente como ${\ {10/ 2}}$

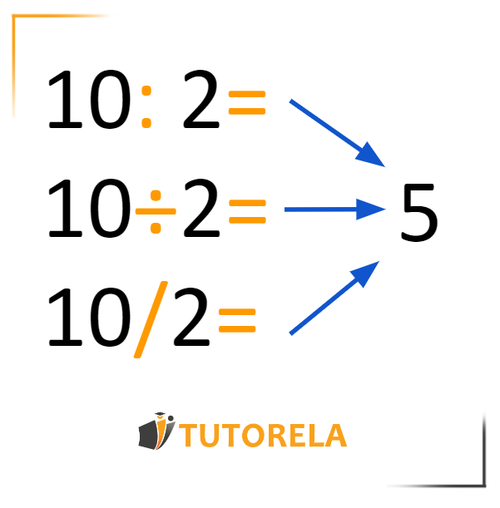
Dos cosas que debemos recordar:

• No se puede dividir entre 0. Para comprobarlo veamos el siguiente ejemplo: ${\ {3:0=}}$
  Para resolverlo, haremos lo siguiente: ${\ {0 \cdot ?=3}}$Es decir, ¿qué número multiplicado por 0 nos dará 3 como resultado? No existe ningún número así, por tanto, no se puede dividir por 0.
   
• Cuando tenemos una línea de fracción es como si hubiera paréntesis en el numerador. Primero resolvemos el numerador y después continuamos con el ejercicio.
  Por ejemplo: 
• ${\ {{10-2 \over 2}= {8 \over 2} = 4}}$

Si te interesa este artículo también te pueden interesar los siguientes artículos:

Fracciones

¿Cómo se reducen las fracciones?

División de potencias de igual base

La propiedad distributiva en el caso de las divisiones

División de números enteros entre paréntesis en los que hay una multiplicación

División de números enteros entre paréntesis en los que hay una división

En el blog de Tutorela encontrarás una variedad de artículos con interesantes explicaciones sobre matemáticas

$(17-7):(55-20)=\frac{10}{33}$

$(9+7):(24+7)=\frac{16}{31}$

$(6+1):(X\times7)=\frac{7}{7X}$

$(2:6):(49:7)=\frac{\frac{1}{3}}{7}$

$(8\times X):(22-8)=\frac{8X}{14}$

• $\ {{20-5} \over {7+3}}=$
• $\ 18:3=$
• $\ 11-3:4=$
• $\ (85+5):10=$
• $\ 11:2+4{1 \over 2}=$
• $\ 0.5-0.1:0.2=$
• $\ {18 \over {18+36}}=$
• $\ {{0.18+0.37} \over {99+13-{2 \over 1}}}=$

Consigna:

Resolver la siguiente ecuación:

$[(3-2+4)^2-2^2]:\frac{(\sqrt{9}\cdot7)}{3}=$

Solución:

En el primer paso resolveremos los corchetes, comenzaremos con las operaciones de suma y resta dentro de los paréntesis internos y luego con las potencias.

$[5^2-4]:\frac{(\sqrt{9}\cdot7)}{3}=$

En el segundo paso resolveremos la raíz en el paréntesis adicional en la fracción

$[5^2-4]:\frac{(3\cdot7)}{3}=$

Resolvemos de acuerdo al orden de las operaciones aritméticas

$[25-4]:\frac{21}{3}=$

$21:7=3$

Respuesta:

$3$

Consigna:

Resolver la siguiente ecuación:

$\frac{(44-3\cdot0)}{11}:4-\frac{3\cdot4+5}{17}=$

Solución:

Primero resolvemos los paréntesis que aparecen en la primera fracción y luego resolvemos según el orden de operaciones aritméticas la ecuación que aparece en la segunda fracción

$\frac{44}{11}:4-\frac{12+5}{17}=$

Continuamos resolviendo

$4:4-\frac{17}{17}=$

$1-1=0$

Respuesta:

$0$

Consigna:

Marca la respuesta correcta

$\frac{7+8-3}{2}:3+4=$

Solución:

Comenzamos a resolver la ecuación que aparece en la fracción de acuerdo al orden de operaciones aritméticas

$\frac{12}{2}:3+4=$

Continuamos resolviendo

$6:3+4=$

$2+4=6$

Respuesta:

$6$

Consigna:

Marca la respuesta correcta

$\frac{36-(4\cdot5)}{8}-3\cdot2=$

Solución:

Comenzamos resolviendo los paréntesis que aparecen en la fracción

$\frac{36-20}{8}-3\cdot2=$

Después continuamos resolviendo de acuerdo al orden de las operaciones aritméticas

$\frac{16}{8}-6=$

$2-6=-4$

Respuesta:

$-4$

Consigna:

Marca la respuesta correcta

$\frac{25+3-2}{13}+5\cdot4=$

Solución:

En el comienzo resolvemos la ecuación que aparece en la fracción de acuerdo con el orden de las operaciones aritméticas

$\frac{26}{13}+5\cdot4=$

Después continuamos con la operación de división de la fracción y el ejercicio de multiplicación

$2+20=22$

Respuesta:

$22$