Ejercicios de Fórmulas de Multiplicación Abreviadas

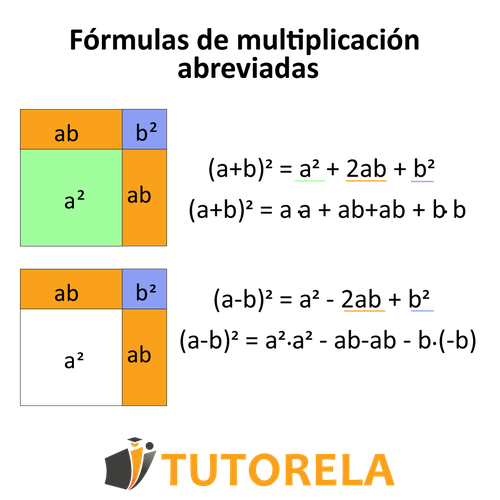
Las fórmulas de multiplicación abreviadas se utilizarán a lo largo de nuestros estudios de matemáticas, desde la escuela primaria hasta la secundaria. En muchos casos, necesitaremos saber cómo abrir o sumar estas ecuaciones para llegar a la solución de varios ejercicios de matemáticas.

Al igual que otros temas de matemáticas, incluso en el caso de las fórmulas de multiplicación abreviadas, no hay nada que temer. La comprensión de las fórmulas y mucha práctica en el tema le brindará un control total. Así que comencemos :)

Estas son las fórmulas básicas de la multiplicación abreviada:

$(X + Y)^2=X^2+ 2XY + Y^2$

$(X - Y)^2=X^2 - 2XY + Y^2$

$(X + Y)\times (X - Y) = X^2 - Y^2$

$(a+b)^3=a^3+3a^2 b+3ab^2+b^3$

$​​​​​​​(a-b)^3=a^3-3a^2 b+3ab^2-b^3$

Probaremos las fórmulas de multiplicación abreviadas mediante la apertura del paréntesis.

$(X + Y)^2 = (X + Y)\times (X+Y) =$

$X^2 + XY + YX + Y^2=$

Puesto que: $XY = YX$

$X^2 + 2XY + Y^2$

$(X - Y)^2 = (X - Y)\times (X-Y) =$

$X^2 - XY - YX + Y^2=$

Puesto que:$XY = YX$

$X^2 - 2XY + Y^2$

$(X + Y)\times (X-Y) =$

$X^2 - XY + YX + Y^2=$

Puesto que: $XY = YX$

$- XY + YX = 0$

$X^2 + 2XY + Y^2$

$(X + 2)^2=X^2 - 8$

$-(X + 2)^2=-X^2 - 8$

$(X + 3)^2=(X-4)\times (X+4)$

$(X + 2)^2=X^2 - 8$

$-(X + 2)^2=-X^2 - 8$

$(X + 3)^2=(X-4)\times (X+4)$