Fórmula para calcular el área del triángulo equilátero:


¿Cuál es el área del triángulo dado?
El cálculo del área del triángulo equilátero es bastante simple, no puedes confundirte demasiado con él, ni siquiera un poco.
Todo lo que debes recordar es la fórmula que te presentaremos a continuación y aplicarla en los triángulos equiláteros:

¡Recuerda!
En los triángulos equiláteros, la altura es también la mediana y la bisectriz.
Por lo tanto, si en la pregunta se da sólo la longitud de la mediana o de la bisectriz podrás deducir, de inmediato, que se trata de la altura que necesitas para colocar en la fórmula.
Y encima de eso, ya que el triángulo es equilátero, en seguida podrás hallar la longitud de la arista (o lado) correspondiente. Simplemente compárala con la arista dada ya que son todas equivalentes.
Practiquemos para que podamos entender aún mejor cómo calcular el área de un triángulo equilátero:
Dado el triángulo

Dado que:
Triángulo equilátero
Altura
¿Cuál es el área del triángulo?
Solución:
A primera vista vemos que tenemos una altura equivalente a y un lado equivalente a .
Coloquemos en la fórmula y obtendremos:
Respuesta:
El área del triángulo es cm2.
¿Sencillo y fácil ¿cierto?
¿Cuál es el área del triángulo del dibujo?
Dado el triángulo ABC.
AC = 10 cm, AD = 3 cm, BC = 11.6 cm
¿Cuál es el área del triángulo?
Halla el área del triángulo mediante los datos de la figura:
que cubre varias situaciones hipotéticas que podrían llegar a confundirte en el examen:
Dado el triángulo equilátero

Dado que:
¿Cuál es el área del triángulo ?
Solución:
Sabemos que para calcular el área del triángulo necesitamos tener la longitud de la altura y del lado correspondiente con el que ésta forma grados.
En este ejercicio no se explicita que es la altura del triángulo, pero sabemos que: es decir, que es la mediana - cruza el lado que toca dividiéndolo en dos partes iguales.
Ya que se trata de un triángulo equilátero, la mediana también es la altura del triángulo y, por lo tanto, podemos utilizarla en la fórmula para el cálculo del área.
Nota extra: Si en lugar del dato que es la mediana hubieran dado que es la bisectriz , también habríamos podido deducir que se trata de la altura, ya que en un triángulo equilátero, la mediana, la altura y la bisectriz coinciden.
Por consiguiente, anotaremos altura del triángulo.
Ahora debemos hallar el largo del lado
Ya que se trata de un triángulo equilátero, todos los lados son iguales, entonces deduciremos de inmediato que
Ahora coloquemos en la fórmula y obtendremos:
Respuesta:
El área del triángulo es es cm2.
Si te interesa este artículo también te pueden interesar los siguientes artículos
En el blog de Tutorela encontrarás una variedad de artículos sobre matemáticas.
¿Cuál es el área del triángulo dado?
Esta pregunta es un poco confusa, debido a que a partir de los datos necesitamos identificar cuáles son relevantes para nosotros y utilizar solo ellos.
Recordando la fórmula para el área de un triángulo:
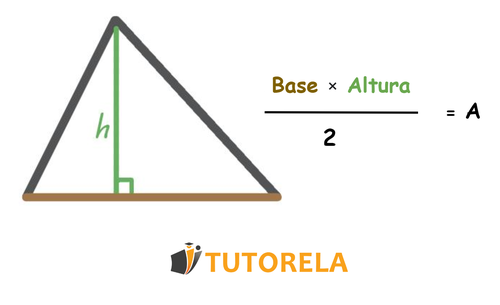 Una altura es una línea recta que sale de un ángulo y forma un ángulo recto con el lado opuesto.
Una altura es una línea recta que sale de un ángulo y forma un ángulo recto con el lado opuesto.
En el dibujo tenemos una altura, de longitud 6.
que baja hasta el lado rojo cuya longitud es 5.
Y por lo tanto, estos son los datos que utilizaremos.
Reemplazamos en la fórmula:
15
¿Cuál es el área del triángulo del dibujo?
Primero identificaremos las partes que necesitamos para poder hallar el área del triángulo.
Fórmula del área del triángulo: altura*lado al que desciende de la altura / 2
Como es un triángulo rectángulo, sabemos que los lados rectos en realidad también son las alturas entre sí, es decir, el lado que mide 5 y el lado que mide 7.
Multiplicamos los catetos y se divide por 2
17.5
Dado el triángulo ABC.
AC = 10 cm, AD = 3 cm, BC = 11.6 cm
¿Cuál es el área del triángulo?
El triángulo que estamos viendo es el triángulo grande - ABC
El triángulo está formado por tres lados AB, BC y CA.
Ahora recordemos lo que necesitamos para el cálculo de un área triangular:
(lado x la altura que desciende del lado)/2
Por lo tanto, lo primero que debemos encontrar es una altura y un lado adecuados.
Se nos da el AC lateral, pero no hay altura que desciende, por lo que no nos sirve.
El lado AB no está dado,
Y así nos quedamos con el lado BC, que está dado.
Por el lado BC desciende la altura AD (los dos forman un ángulo de 90 grados).
Se puede argumentar que BC es también una altura, pero si profundizamos parece que CD puede ser una altura en el triángulo ADC,
y BD es una altura en el triángulo ADB (ambos son los lados de un triángulo rectángulo, por lo tanto son la altura y el lado).
Como no sabemos si el triángulo es isósceles o no, tampoco es posible saber si CD=DB, o cuál es su razón, y esta teoría falla.
Recordemos nuevamente la fórmula del área triangular y reemplacemos los datos que tenemos en la fórmula:
(lado* la altura que desciende del lado)/2
Ahora reemplazamos los datos existentes en esta fórmula:
17.4
Halla el área del triángulo (tenga en cuenta que esto no siempre es posible)
La fórmula para calcular el área de un triángulo es:
(lado * altura correspondiente al lado) / 2
Observa que en el triángulo que se nos proporciona, tenemos la longitud del lado pero no la altura.
Es decir, no tenemos datos suficientes para realizar el cálculo.
No se puede calcular
Calcula el área del triángulo siguiente:
La fórmula de cálculo del área triangular es:
(el lado * la altura del lado que desciende al lado) /2
Es decir:
Ahora reemplazamos los datos existentes:
10
Halla el área del triángulo mediante los datos de la figura:
Halla el área del triángulo mediante los datos de la figura:
Halla el área del triángulo mediante los datos de la figura: