La fórmula para calcular el área de un triángulo de cualquier tipo:
altura por base dividido entre .
Como hallar el área de un triángulo:

La fórmula para calcular el área de un triángulo de cualquier tipo:
altura por base dividido entre .


Completa la oración
Para encontrar el área de un triángulo rectángulo, se debe multiplicar a _ entre sí y dividir por 2.
Si aplicamos la fórmula, multiplicamos la altura ( cm) por la longitud de la base ( cm).
Al multiplicar por , obtenemos , resultado que debemos dividir entre .
entre equivale a .
Por tanto, el área de este triángulo es .
Tanto si te estás preparando para un examen como si dentro de poco tienes las pruebas de acceso a la universidad, es imprescindible saber cómo calcular el área de un triángulo, rectángulo, isósceles, etc.
Se trata de una de las preguntas que más sale en los exámenes de geometría, así que ¿cómo se calcula un área triangular?
¡Esta guía aclarará todas tus dudas!
Se trata de una de las preguntas que más sale en los exámenes de geometría, así que ¿cómo se calcula un área triangular?
¡Esta guía aclarará todas tus dudas!
Calcula el área del triángulo siguiente:
Calcula el área del triángulo siguiente:
Halla el área del triángulo mediante los datos de la figura:
Un triángulo es una figura geométrica compuesta por tres lados que dan lugar a tres ángulos y tres vértices.
Los vértices del triángulo se señalan con las letras y y de su unión nacen los lados ().
distintos tipos de triángulos y algunos de ellos incluso comparten características (te daremos información al respecto más adelante en este artículo).

Antes de abordar los distintos tipos de triángulo que existen y cómo calcular su área,
debemos conocer en primer lugar los términos que se suelen emplear cuando hablamos de un área triangular.

Halla el área del triángulo mediante los datos de la figura:
Calcula el área del triángulo siguiente:
¿Cuál es el área del triángulo dado?
Uno de los consejos más útiles que te pueden servir a la hora de calcular el área de un triángulo (y así resolver el problema) es comprender que un triángulo es medio cuadrado.
Hay triángulos que son fácilmente distinguibles como «medio cuadrado» debido a su forma, como, por ejemplo, el triángulo rectángulo isósceles.
No obstante, es importante señalar que aquellos triángulos que a priori no parecen ser «medios cuadrados» también lo son, ya que este es uno de los rasgos que los caracterizan.
¿Cuál es la siguiente fase? Calcular el área del triángulo.
La fórmula que se utiliza para calcular el área de un triángulo es la siguiente:
altura por base dividido entre .

Información:
Solución:
Si aplicamos la fórmula, multiplicamos la altura ( cm) por la longitud de la base ( cm).
Al multiplicar por , obtenemos , resultado que debemos dividir entre .
entre equivale a .
Por tanto, el área de este triángulo es .

Dado el triángulo ABC.
AC = 10 cm, AD = 3 cm, BC = 11.6 cm
¿Cuál es el área del triángulo?
Calcula el área del triángulo ABC mediante los datos del dibujo:
Halla el área del triángulo (tenga en cuenta que esto no siempre es posible)
Información:
Solución:
De nuevo, si aplicamos la fórmula, multiplicamos la altura ( cm) por la longitud de la base ( cm).
Al multiplicar por , obtenemos , resultado que debemos dividir entre .
entre equivale a .
Por tanto, el área de este triángulo es .
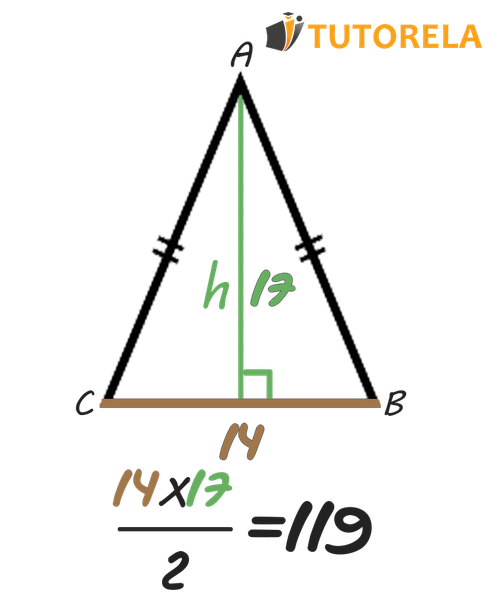
Información:
Solución:
Si aplicamos la fórmula, multiplicamos la altura ( cm) por la longitud de la base ( cm).
Al multiplicar por obtenemos , resultado que debemos dividir entre .
entre equivale a .
Por tanto, el área de este triángulo es .

Al hacer clic en el enlace puede encontrar más información sobre un triángulo escaleno
Halla el área del triángulo (tenga en cuenta que esto no siempre es posible)
Halla el área del triángulo (ten en cuenta que esto no siempre es posible)
Calcula el área del triángulo siguiente:
Información:
Atención: en un triángulo rectángulo, usando el Teorema de Pitágoras podemos observar que la base y la altura coinciden en ser los catetos de dicho triángulo rectángulo.
Solución:
Si aplicamos la fórmula, multiplicamos la altura ( cm) por la longitud de la base ( cm).
Al multiplicar por obtenemos , resultado que debemos dividir entre .
entre equivale a .
Por tanto, el área de este triángulo es .

Información:
Atención:
En un triángulo obtuso, la altura se encuentra fuera del triángulo.
Esto quiere decir que debemos extender la recta de la base desde el punto al punto para hallar la altura.
De esta manera se genera un triángulo rectángulo donde la altura que buscamos es el lado .
No obstante, recuerda que como se trata de calcular el área del triángulo obtuso, tan solo tendremos que considerar el lado como la base.
Solución:
En este caso también, si aplicamos la fórmula, multiplicamos la altura ( cm) por la longitud de la base del triángulo cuya área queremos hallar.
Al multiplicar por obtenemos , resultado que debemos dividir entre .
entre equivale a .
Por tanto, el área de este triángulo es .

Calcula el área del triángulo siguiente:
Halla el área del triángulo (ten en cuenta que esto no siempre es posible)
Completa la oración
Para encontrar el área de un triángulo rectángulo, se debe multiplicar a _ entre sí y dividir por 2.
¿Cuál es la fórmula de Herón y para qué sirve?
La fórmula de Herón, nos ayuda a calcular el área de un triángulo si conocemos sus tres lados y y la fórmula la podemos denotar de la siguiente manera:
En este caso indica el perímetro del triangulo pero divido entre recordemos que el perímetro es la suma de todos su lados, en este caso se suman sus tres lados, y después calculamos la mitad de esta suma.

Tarea:

Consigna verbal
En el parque de un hotel quieren construir una piscina especial de forma triangular.
El largo de la piscina es de m.
El ancho de la piscina es de m.
La piscina está cubierta con baldosas de m de largo y m de ancho.
Pregunta:
¿Cuántas baldosas se necesitan para cubrir el área de la piscina?
Solución:
Para saber cuántas baldosas se necesitan calcularemos el área triangular y el área de cada baldosa y luego dividiremos.
El resultado es igual a la cantidad de baldosas que se necesitan.
En un triángulo su largo es igual a su altura y su ancho es igual a la base del triángulo
Dado=h=largo= metros
Dado=base=ancho= metros
Dado que el largo son metros
El ancho: metros
Área de la baldosa
Respuesta:
baldosas
Calcula el área del triángulo siguiente:
Calcula el área del triángulo siguiente:
Halla el área del triángulo mediante los datos de la figura:
Tarea:
El triángulo es rectángulo
El área del triángulo es igual a
Calcula a y el largo del lado

Solución:
Utilizamos la fórmula para calcular el área del triángulo rectángulo:
Y compara la expresión con el área del triángulo
Duplicar la ecuación por el denominador común significa que multiplicamos por
Abrimos los paréntesis antes de la propiedad distributiva
/
/
Reemplazamos en la expresión y
encontramos:
Respuesta:
Tarea:

Dado el triángulo
El largo del lado es igual a .
El área del triángulo es igual a cm²
Calcular la altura
Solución:
Utilizamos la fórmula para calcular el área del triángulo.
Presta atención: ¡en el triángulo obtusángulo, su altura se encuentra por fuera del triángulo!
Duplicar la ecuación por un denominador común.
/
Divide la ecuación por el coeficiente de .
/
Respuesta:
La longitud de la altura es igual a .
Halla el área del triángulo mediante los datos de la figura:
Calcula el área del triángulo siguiente:
¿Cuál es el área del triángulo dado?
Tarea:

Dado el triángulo rectángulo
El perímetro del triángulo es igual a .
Dado:
Calcular el área del triángulo
Solución:
Dado el perímetro del triángulo igual a .
Desde aquí podemos calcular a .
/
Ahora podemos calcular el área del triángulo
Prestar atención: hablamos de un triángulo obtusángulo por lo tanto su altura es .
Usamos la fórmula para calcular el área del triángulo:
Respuesta:
El área del triángulo es igual a .
El triángulo es isósceles
es la altura del lado
Dado que
La longitud de la altura es mayor en un que la longitud del lado .

Tarea:
Calcular el área del triángulo
Solución:
Dado que es un triángulo isósceles, y por lo tanto mediana, y por eso entonces .
La altura es mayor en que el largo de .
Es decir:
De aquí, el área del triángulo :
Respuesta:
El área del triángulo es igual a .
Dado el triángulo ABC.
AC = 10 cm, AD = 3 cm, BC = 11.6 cm
¿Cuál es el área del triángulo?
Calcula el área del triángulo ABC mediante los datos del dibujo:
Halla el área del triángulo (tenga en cuenta que esto no siempre es posible)
El resto de los términos, como mediana, bisectriz, etc., se emplean cuando nos falta algún dato. Estos términos son una ayuda que nos permitirá hallar nuevos datos cuando tengamos que resolver un problema en el que nos falta información.
Muchos alumnos experimentan una sensación de fracaso examen tras examen, aunque el éxito en este aspecto es subjetivo. Al comparar, debemos tomar en consideración nuestros logros y dejar a un lado las notas del resto de compañeros. Muchas veces, el problema no es que no nos sepamos la lección o que no hayamos comprendido cómo calcular el área de un triángulo, sino que no nos hemos preparado bien para el examen.
Por poner un ejemplo: imagina un pastelero excelente que sabe muchas recetas, conoce los productos y logra crear pasteles verdaderamente deliciosos. Si no hubiese practicado y no se hubiese preparado bien (comprar los productos y los electrodomésticos que le hacen falta, encontrar buenas recetas y tener paciencia con los tiempos indicados), no habría conseguido buenos resultados. Así ocurre también los estudiantes; una buena preparación es clave.
Halla el área del triángulo (tenga en cuenta que esto no siempre es posible)
Halla el área del triángulo (ten en cuenta que esto no siempre es posible)
Calcula el área del triángulo siguiente:
Tu destreza a la hora de estudiar es tan importante como el aprendizaje de los contenidos. Por ello, el cronómetro puede ser tu gran aliado. Te recomendamos que adoptes su uso desde ya; por ejemplo, el que viene en tu móvil es más que suficiente.
Durante todo el año (y no solo antes de los exámenes), una vez hayas te hayas aprendido la lección, es recomendable practicar y resolver problemas con un cronómetro. ¿Por qué?
Calcula el área del triángulo siguiente:
Halla el área del triángulo (ten en cuenta que esto no siempre es posible)
Completa la oración
Para encontrar el área de un triángulo rectángulo, se debe multiplicar a _ entre sí y dividir por 2.
A muchos estudiantes les cuesta digerir el hecho de haber sacado una nota baja y, principalmente, la decepción que suele acompañarlo. Es muy importante que sepas que, cuanto más dejes que esto te afecte, peor será el impacto en tus logros académicos.
La nota que sacas en un examen es una especie de feedback que te indica qué estás haciendo bien y qué podrías mejorar. ¿Cómo puede este feedback cambiar la forma en que estudias?
Nosotros no lo recomendamos y la razón es muy simple: una clase particular es «particular», es decir, está adaptada a tus necesidades. En el momento en que dos amigos estudian en una misma clase particular, uno de ellos tendrá que adaptarse al ritmo del otro.
Por ello, la idea adaptación a las necesidades del alumno de una «clase particular» se diluye. Dicho esto, si tanto a ti como a tu amigo os resulta difícil un mismo tema (por ejemplo, cómo calcular el área de un triángulo), podéis coger una clase particular conjunta.
Calcula el área del triángulo siguiente:
Calcula el área del triángulo siguiente:
Halla el área del triángulo mediante los datos de la figura:
Si en el examen te preguntan sobre un triángulo rectángulo, por ejemplo, podrás multiplicar los catetos (los lados del triángulo que no son la base) y dividirlos entre 2. Esta forma es, en muchas ocasiones, un atajo para llegar a la solución. Por eso es importante que te sepas la fórmula y esta característica específica de este triángulo.
Además, si te preguntan sobre un triángulo isósceles, debes saber que tanto la bisectriz como la mediana se consideran la altura del triángulo. Por eso, estos datos pueden servirte como atajo para llegar antes a la solución, ya que, gracias a ellos, podrás contestar a la pregunta de cuál es el área del triángulo.
Si estás interesado en aprender a calcular áreas de otras formas geométricas, puedes ingresar a uno de los siguientes artículos:
En la página web de Tutorela encontrarás una variedad de artículos sobre matemáticas.
Halla el área del triángulo mediante los datos de la figura:
Calcula el área del triángulo siguiente:
¿Cuál es el área del triángulo dado?
Muchas veces, el estudio de las matemáticas despierta algo de ansiedad entre los alumnos de secundaria y de niveles posteriores. Una clase particular de matemáticas es ideal para aquellos que quieren sacar buenas notas en sus exámenes, pero no saben cómo.
Una clase particular se centra en un aspecto determinado y, en su transcurso, no solo se hacen ejercicios:
Antes, las clases particulares de matemáticas o cualquier otra asignatura tenían lugar en la casa del alumno o del profesor. Hoy en día, también es posible tener una muy buena clase particular en línea. Se trata de una gran posibilidad de afianzar los contenidos de matemáticas en los que estamos un poco más verdes a la vez que el aprendizaje se produce en las condiciones más cómodas y en las horas que mejor convengan tanto al alumno como al profesor.
Los triángulos y otras formas geométricas son aspectos a los que el alumno se expone ya desde sus primeros años en el instituto. Sus notas en matemáticas son las que marcan el ritmo de aprendizaje del alumno y son decisivas a la hora de escoger esta asignatura en etapas más avanzadas de la educación secundaria. Muchas veces, la dificultad de las matemáticas no es producto de una baja capacidad, sino que surge de métodos de aprendizaje erróneos que no ayudan al alumno a comprender el contenido. Un profesor particular de matemáticas trabaja codo con codo con el alumno, de manera progresiva y centrándose en el proceso de aprendizaje para conseguir que, al final, el alumno haya comprendido los contenidos.
Dado el triángulo ABC.
AC = 10 cm, AD = 3 cm, BC = 11.6 cm
¿Cuál es el área del triángulo?
Calcula el área del triángulo ABC mediante los datos del dibujo:
Halla el área del triángulo (tenga en cuenta que esto no siempre es posible)
Calcula el área del triángulo siguiente:
La fórmula de cálculo del área triangular es:
(el lado * la altura del lado que desciende al lado) /2
Es decir:
Ahora reemplazamos los datos existentes:
10
¿Cuál es el área del triángulo dado?
Esta pregunta es un poco confusa, debido a que a partir de los datos necesitamos identificar cuáles son relevantes para nosotros y utilizar solo ellos.
Recordando la fórmula para el área de un triángulo:
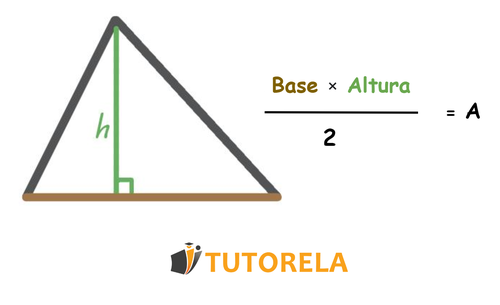 Una altura es una línea recta que sale de un ángulo y forma un ángulo recto con el lado opuesto.
Una altura es una línea recta que sale de un ángulo y forma un ángulo recto con el lado opuesto.
En el dibujo tenemos una altura, de longitud 6.
que baja hasta el lado rojo cuya longitud es 5.
Y por lo tanto, estos son los datos que utilizaremos.
Reemplazamos en la fórmula:
15
Dado el triángulo ABC.
AC = 10 cm, AD = 3 cm, BC = 11.6 cm
¿Cuál es el área del triángulo?
El triángulo que estamos viendo es el triángulo grande - ABC
El triángulo está formado por tres lados AB, BC y CA.
Ahora recordemos lo que necesitamos para el cálculo de un área triangular:
(lado x la altura que desciende del lado)/2
Por lo tanto, lo primero que debemos encontrar es una altura y un lado adecuados.
Se nos da el AC lateral, pero no hay altura que desciende, por lo que no nos sirve.
El lado AB no está dado,
Y así nos quedamos con el lado BC, que está dado.
Por el lado BC desciende la altura AD (los dos forman un ángulo de 90 grados).
Se puede argumentar que BC es también una altura, pero si profundizamos parece que CD puede ser una altura en el triángulo ADC,
y BD es una altura en el triángulo ADB (ambos son los lados de un triángulo rectángulo, por lo tanto son la altura y el lado).
Como no sabemos si el triángulo es isósceles o no, tampoco es posible saber si CD=DB, o cuál es su razón, y esta teoría falla.
Recordemos nuevamente la fórmula del área triangular y reemplacemos los datos que tenemos en la fórmula:
(lado* la altura que desciende del lado)/2
Ahora reemplazamos los datos existentes en esta fórmula:
17.4
Calcula el área del triángulo ABC mediante los datos del dibujo:
En primer lugar, recordemos la fórmula para el área de un triángulo:
(el lado * la altura del desciende al lado) /2
En la pregunta tenemos tres datos, ¡pero uno de ellos es redundante!
Solo tenemos una altura, la línea que forma un ángulo de 90 grados - AD,
El lado al que desciende la altura es CB,
Por lo tanto, podemos usarlos en nuestro cálculo:
36 cm²
¿Cuál es el área del triángulo del dibujo?
Primero identificaremos las partes que necesitamos para poder hallar el área del triángulo.
Fórmula del área del triángulo: altura*lado al que desciende de la altura / 2
Como es un triángulo rectángulo, sabemos que los lados rectos en realidad también son las alturas entre sí, es decir, el lado que mide 5 y el lado que mide 7.
Multiplicamos los catetos y se divide por 2
17.5